
【题目】设函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(2)设![]() ,且
,且![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
①证明![]() 恰有两个零点;
恰有两个零点;
②设![]() 如为
如为![]() 的极值点,
的极值点,![]() 为
为![]() 的零点,且
的零点,且![]() ,证明:
,证明:![]() .
.
【答案】(1)证明见解析;
(2)①证明见解析;②证明见解析;
【解析】
(1)将条件转化,构造函数![]() ,通过导数证明,当
,通过导数证明,当![]() 时,
时,![]() 即可;
即可;
(2)先求得![]() ,先判断
,先判断![]() 的增减性,设导数为零的点为
的增减性,设导数为零的点为![]() ,可证
,可证![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,再结合(1)的性质可得
内单调递减,再结合(1)的性质可得 ,即
,即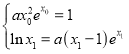 ,将
,将![]() 代换可得
代换可得![]() ,再结合(1)的性质放缩,即可求证
,再结合(1)的性质放缩,即可求证
令![]()
![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上递减,
上递减,
又![]() 在
在![]() 上连续,
上连续,
所以当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]()
(2)证明:①![]() ,得
,得![]()
令![]() ,由
,由![]() ,
,
可知![]() 在
在![]() 内单调递减,又
内单调递减,又![]() ,且
,且
![]()
![]() .
.
故![]() 在
在![]() 有唯一解,从而
有唯一解,从而![]() 在
在![]() 内有唯一解,
内有唯一解,
不妨设为![]() ,则
,则![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内单调递减,
内单调递减,
因此![]() 是
是![]() 的唯一极值点.
的唯一极值点.
由(1)知![]() .从而
.从而
![]()
![]()
又因为![]() ,所以
,所以![]() 在
在![]() 内有唯一零点.
内有唯一零点.
又![]() 在
在![]() 内有唯一零点
内有唯一零点![]() ,从而
,从而![]() 在
在![]() 内恰有两个零点.
内恰有两个零点.
②由题意, ,即
,即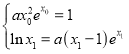 ,
,
从而![]() ,即
,即![]() .
.
因为当![]() 时,
时,![]() ,又
,又![]() ,故
,故![]()
两边取对数,得![]() ,于是
,于是![]()
整理得![]() .
.


科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一正方体的平面展开图,在这个正方体中,有以下结论:①![]() ,②CF与EN所成的角为
,②CF与EN所成的角为![]() ,③
,③![]() //MN ,④二面角
//MN ,④二面角![]() 的大小为
的大小为![]() ,其中正确的个数是( )
,其中正确的个数是( )
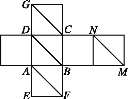
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,动点
中,动点![]() (其中
(其中![]() )到点
)到点![]() 的距离的
的距离的![]() 倍与点
倍与点![]() 到直线
到直线![]() 的距离的
的距离的![]() 倍之和记为
倍之和记为![]() ,且
,且![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人参加某种选拔测试,在备选的10道题中,甲答对其中每道题的概率都是![]() ,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
,乙能答对其中的8道题,规定每次考试都从备选的10道题中随机抽出4道题进行测试,只有选中的4个题目均答对才能入选.
(1)求甲恰有2个题目答对的概率;
(2)求乙答对的题目数X的分布列;
(3)试比较甲,乙两人平均答对的题目数的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将曲线![]() 上每个点的横坐标伸长为原来的
上每个点的横坐标伸长为原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
B.![]() 在
在![]() 上的值域为
上的值域为![]()
C.![]() 的图象关于点
的图象关于点![]() 对称
对称
D.![]() 的图象可由
的图象可由![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com