
分析 (Ⅰ)由题意利用二项式系数的性质求得r的值.
(Ⅱ)利用通项公式求得T5=${C}_{14}^{4}$•210•(-x)4,倒数第5项,即T11=${C}_{14}^{10}$•24•(-x)10,根据这两项相等,解得x的值.
解答 解:(Ⅰ)由题意知,2r-1=r+1-1或2r-1+r=14,解得r=1(舍去) 或r=5,
故r的值为5.
(Ⅱ)由题意可得Tr=${C}_{14}^{r-1}$•215-r•(-x)r-1,当r=5时,T5=${C}_{14}^{4}$•210•(-x)4,
倒数第5项,即T11=${C}_{14}^{10}$•24•(-x)10,
由题意 ${C}_{14}^{4}$•210•(-x)4=${C}_{14}^{10}$•24•(-x)10,解得x=±2.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.
在△ABC中,∠BAC=45°,∠ABC=60°,O为三角形的外心,以线段OB,OC为邻边作平行四边形,第四个顶点为D,再以OA,OD为邻边作平行四边形,它的第四个顶点为H.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
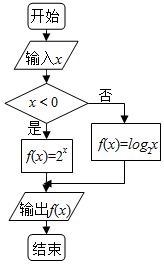 如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].
如图程序框图运行后,如果输出的函数值在区间[-2,$\frac{1}{2}$]内,则输入的实数x的取值范围是(-∞,-1]∪[$\frac{1}{4}$,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 30 | C. | 36 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影部分的概率为$\frac{1}{4}$,那么△ABC的面积是8π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).
如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
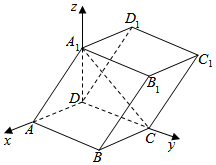 如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ANCD所成角为θ(0<θ<$\frac{π}{2}$),∠ADC=2θ
如图,在平行六面体ABCD-A1B1C1D1中,AD=1,CD=2,A1D⊥平面ABCD,AA1与底面ANCD所成角为θ(0<θ<$\frac{π}{2}$),∠ADC=2θ查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com