
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 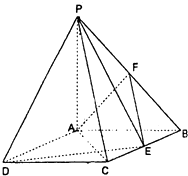
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
【答案】
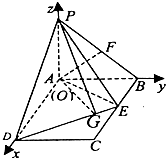
(1)解:分别以AD、AB、AP所在直线为x、y、z轴,建立如图所示空间坐标系
则可得P(0,0,1),B(0,1,0),F(0, ![]() ,
, ![]() ),D(
),D( ![]() ,0,0)
,0,0)
设BE=x,则E(x,1,0)
∴ ![]() =(x,1,﹣1)
=(x,1,﹣1)
得 ![]() =x0+1×
=x0+1× ![]() +(﹣1)×
+(﹣1)× ![]() =0
=0
可得 ![]() ,即AF⊥PE成立
,即AF⊥PE成立
(2)解:求出 ![]() =(
=( ![]() ,0,﹣1),设平面PDE的一个法向量为
,0,﹣1),设平面PDE的一个法向量为 ![]()
则 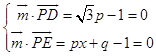 ,得
,得 ![]()
∵PA与平面PDE所成角的大小为45°, ![]() =(0,0,1)
=(0,0,1)
∴sin45°= 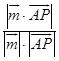 =
= ![]() ,得
,得 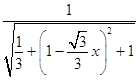 =
= ![]()
解之得x= ![]() 或x=
或x= ![]()
∵BE=x ![]() ,
,
∴BE= ![]() ,即当BE等于
,即当BE等于 ![]() 时,PA与平面PDE所成角的大小为45°.
时,PA与平面PDE所成角的大小为45°.
【解析】(1)建立如图所示空间坐标系,得出P、B、F、D的坐标.设BE=x得E(x,1,0),算出 ![]() 的坐标,得出
的坐标,得出 ![]() ,由此可得无论点E在BC边的何处,都有PE⊥AF;(2)利用垂直向量数量积为零的方法,算出
,由此可得无论点E在BC边的何处,都有PE⊥AF;(2)利用垂直向量数量积为零的方法,算出 ![]() 是平面PDE的一个法向量,结合
是平面PDE的一个法向量,结合 ![]() =(0,0,1)与题中PA与平面PDE所成角,利用空间向量夹角公式建立关于x的方程,解出x的值即可得到PA与平面PDE所成角的大小为45°时,BE的长.
=(0,0,1)与题中PA与平面PDE所成角,利用空间向量夹角公式建立关于x的方程,解出x的值即可得到PA与平面PDE所成角的大小为45°时,BE的长.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行,以及对用空间向量求直线与平面的夹角的理解,了解设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: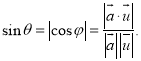 .
.


科目:高中数学 来源: 题型:
【题目】某科技博览会展出的智能机器人有 A,B,C,D 四种型号,每种型号至少有 4 台.要求每 位购买者只能购买1台某种型号的机器人,且购买其中任意一种型号的机器人是等可能的.现在有 4 个人要购买机器人.
(Ⅰ)在会场展览台上,展出方已放好了 A,B,C,D 四种型号的机器人各一台,现把他们 排成一排表演节目,求 A 型与 B 型相邻且 C 型与 D 型不相邻的概率;
(Ⅱ)设这 4 个人购买的机器人的型号种数为ξ,求ξ 的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,手机已经成为人们日常生活中不可缺少的产品,手机的功能也日趋完善,已延伸到了各个领域,如拍照,聊天,阅读,缴费,购物,理财,娱乐,办公等等,手机的价格差距也很大,为分析人们购买手机的消费情况,现对某小区随机抽取了200人进行手机价格的调查,统计如下:
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
(Ⅰ)完成关于人们使用手机的价格和年龄的2×2列联表,再判断能否在犯错误的概率不超过0.025的前提下,认为人们使用手机的价格和年龄有关?
(Ⅱ)从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况,设3人中年龄在45岁及以下的人数为随机变量X,求随机变量X的分布列及数学期望.
附K2= ![]()
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学文化知识竞赛培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下: 甲:8281797895889384
乙:9295807583809085
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加正式比赛,从所抽取的两组数据分析,你认为选派哪位同学参加较为合适?并说明理由;
(Ⅲ)若对甲同学在今后的3次测试成绩进行预测,记这3次成绩中高于80分的次数为ξ(将甲8次成绩中高于80分的频率视为概率),求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=f( ![]() )且当x∈[
)且当x∈[ ![]() ,1]时,f(x)=lnx,若当x∈[
,1]时,f(x)=lnx,若当x∈[ ![]() ]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
A.[﹣ ![]() ,0]
,0]
B.[﹣πlnπ,0]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=﹣ln(1﹣x),函数f(x)= ![]() ,若f(2﹣x2)>f(x),则x的取值范围是( )
,若f(2﹣x2)>f(x),则x的取值范围是( )
A.(﹣∞,﹣2)∪(1,+∞)
B.(﹣∞,1)∪(2,+∞)
C.(﹣2,1)
D.(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c. (Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 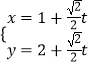 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ. (Ⅰ)求直角坐标下圆C的标准方程;
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ. (Ⅰ)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com