【答案】
分析:(Ⅰ)由题设条件知a
2=2b
2,再由直线l:x-y+2=0与圆x
2+y
2=b
2相切,知
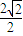
=b,由此可求出椭圆C
1的方程.
(Ⅱ)由MP=MF
2,知动点M到定直线l
1:x=-2的距离等于它到定点F
2(2,0)的距离,由此可求出点M的轨迹C
2的方程.
(Ⅲ)当直线AC的斜率存在且不为零时,设直线AC的斜率为k,A(x
1,y
1),C(x
2,y
2),则直线AC的方程为y=k(x-2),联立
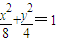
及y=k(x-2)得(1+2k
2)x
2-8k
2x+8k
2-8=0.然后利用根与系数的关系结合题设条件进行求解.
解答:解:(Ⅰ)∵e=
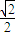
,∴e
2=
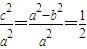
,∴a
2=2b
2∵直线l:x-y+2=0与圆x
2+y
2=b
2相切
∴

=b,∴b=2,b
2=4,∴a
2=8,
∴椭圆C
1的方程是
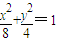
(3分)
(Ⅱ)∵MP=MF
2,
∴动点M到定直线l
1:x=-2的距离等于它到定点F
2(2,0)的距离,
∴动点M的轨迹C是以l
1为准线,F
2为焦点的抛物线
∴点M的轨迹C
2的方程为y
2=8x(6分)
(Ⅲ)当直线AC的斜率存在且不为零时,设直线AC的斜率为k,
A(x
1,y
1),C(x
2,y
2),则直线AC的方程为y=k(x-2)
联立
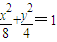
及y=k(x-2)得(1+2k
2)x
2-8k
2x+8k
2-8=0
所以x
1+x
2=
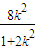
,x
1x
2=
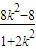
|AC|=
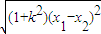
=
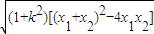
=
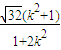
.(8分)
由于直线BD的斜率为-
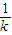
,用-
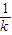
代换上式中的k可得|BD|=
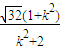
∵AC⊥BD,
∴四边形ABCD的面积为S=

|AC|•|BD|=
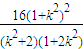
..(10分)
由(1+2k
2)(k
2+2)≤[
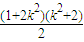
]
2=[

]
2所以S≥
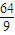
,当1+2k
2=k
2+2时,即k=±1时取等号.(11分)
易知,当直线AC的斜率不存在或斜率为零时,四边形ABCD的面积S=8
综上可得,四边形ABCD面积的最小值为
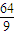
(12分)
点评:本题考查圆锥曲线和直线的位置关系和综合应用,解题时要认真审题,注意韦达定理的合理运用.

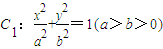 的离心率为
的离心率为 ,直线
,直线 与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切.
与以原点为圆心、以椭圆C1的短半轴长为半径的圆相切.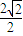 =b,由此可求出椭圆C1的方程.
=b,由此可求出椭圆C1的方程.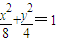 及y=k(x-2)得(1+2k2)x2-8k2x+8k2-8=0.然后利用根与系数的关系结合题设条件进行求解.
及y=k(x-2)得(1+2k2)x2-8k2x+8k2-8=0.然后利用根与系数的关系结合题设条件进行求解.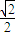 ,∴e2=
,∴e2=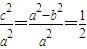 ,∴a2=2b2
,∴a2=2b2 =b,∴b=2,b2=4,∴a2=8,
=b,∴b=2,b2=4,∴a2=8,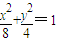 (3分)
(3分)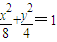 及y=k(x-2)得(1+2k2)x2-8k2x+8k2-8=0
及y=k(x-2)得(1+2k2)x2-8k2x+8k2-8=0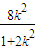 ,x1x2=
,x1x2=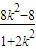
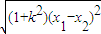 =
=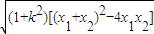 =
=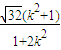 .(8分)
.(8分)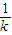 ,用-
,用-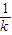 代换上式中的k可得|BD|=
代换上式中的k可得|BD|=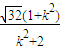
 |AC|•|BD|=
|AC|•|BD|=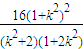 ..(10分)
..(10分)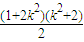 ]2=[
]2=[ ]2
]2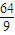 ,当1+2k2=k2+2时,即k=±1时取等号.(11分)
,当1+2k2=k2+2时,即k=±1时取等号.(11分)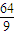 (12分)
(12分)

 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: