
【题目】(2017·合肥市质检)已知点F为椭圆E: ![]() (a>b>0)的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
(a>b>0)的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线![]() 与椭圆E有且仅有一个交点M.
与椭圆E有且仅有一个交点M.
(1)求椭圆E的方程;
(2)设直线![]() 与y轴交于P,过点P的直线l与椭圆E交于不同的两点A,B,若λ|PM|2=|PA|·|PB|,求实数λ的取值范围.
与y轴交于P,过点P的直线l与椭圆E交于不同的两点A,B,若λ|PM|2=|PA|·|PB|,求实数λ的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由两焦点与短轴的一个顶点构成一个等边三角形,直线![]() 与椭圆有且仅有一个交点可得关于
与椭圆有且仅有一个交点可得关于![]() ,
, ![]() 的方程组,求出
的方程组,求出![]() ,
, ![]() 的值,即可得到椭圆的方程;(2)由(1)求得
的值,即可得到椭圆的方程;(2)由(1)求得![]() 坐标,得到
坐标,得到![]() 的值,当直线
的值,当直线![]() 与
与![]() 轴垂直时,直接由
轴垂直时,直接由![]() ,求得
,求得![]() 值;当直线
值;当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,利用判别式大于
,联立直线方程与椭圆方程,利用判别式大于![]() 求得
求得![]() 的取值范围,再由根与系数的关系,结合
的取值范围,再由根与系数的关系,结合![]() ,把
,把![]() 用含有
用含有![]() 的表达式表示,则实数
的表达式表示,则实数![]() 的取值范围可求.
的取值范围可求.
试题解析:(1)由题意,得a=2c,b=![]() c,则椭圆E为
c,则椭圆E为![]() .
.
由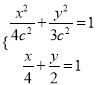 ,得x2-2x+4-3c2=0.
,得x2-2x+4-3c2=0.
∵直线![]() 与椭圆E有且仅有一个交点M,
与椭圆E有且仅有一个交点M,
∴Δ=4-4(4-3c2)=0c2=1,
∴椭圆E的方程为![]() .
.
(2)由(1)得M![]() ,
,
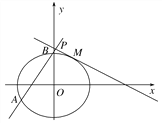
∵直线![]() 与y轴交于P(0,2),
与y轴交于P(0,2),
∴|PM|2=![]() ,
,
当直线l与x轴垂直时,
|PA|·|PB|=(2+![]() )×(2-
)×(2-![]() )=1,
)=1,
∴λ|PM|2=|PA|·|PB|λ=![]() ,
,
当直线l与x轴不垂直时,设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),
由![]() (3+4k2)x2+16kx+4=0,
(3+4k2)x2+16kx+4=0,
依题意得,x1x2=![]() ,且Δ=48(4k2-1)>0,
,且Δ=48(4k2-1)>0,
∴|PA|·|PB|=(1+k2)x1x2=(1+k2)·![]() =1+
=1+![]() =
=![]() λ,
λ,
∴λ=![]() (1+
(1+![]() ),
),
∵k2>![]() ,∴
,∴![]() <λ<1.
<λ<1.
综上所述,λ的取值范围是[![]() ,1).
,1).


科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;(Ⅱ)若c=![]() ,△ABC的面积为
,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+b图象上的点P(2,1)关于直线y=x的对称点Q在函数g(x)=lnx+a上.
(Ⅰ)求函数h(x)=g(x)-f(x)的最大值;
(Ⅱ)对任意x1∈[1,e],x2∈![]() ,是否存在实数k,使得不等式
,是否存在实数k,使得不等式![]() 成立,若存在,请求出实数k的取值范围;若不存在,请说明理由.
成立,若存在,请求出实数k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张纸的长、宽分别为2![]() a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).
a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).

①该多面体是三棱锥;②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数y=f(x)满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;②直线x=-4为函数y=f(x)图象的一条对称轴;③函数y=f(x)在[8,10]上单调递增;④若关于x的方程f(x)=m在[-6,-2]上的两根分别为x1,x2,则x1+x2=-8.
其中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ex(ln x-a)(e是自然对数的底数,
e=2.71 828…).
(1)若y=f(x)在x=1处的切线方程为y=2ex+b,求a,b的值.
(2)若函数f(x)在区间![]() 上单调递减,求实数a的取值范围.
上单调递减,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知△ABC中,角A,B,C所对的边分别为a,b,c,且3a2+ab-2b2=0.
(Ⅰ)若B=![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若sin A+3sin C=3sin B,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
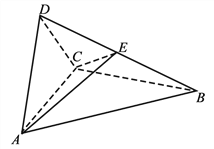
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员x名.
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求x的值;
(Ⅱ)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择,求该客户最终聘请的家政服务员中既有A类又有B类的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com