
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若对于任意的![]() 恒成立,求满足条件的实数m的最小值M .
恒成立,求满足条件的实数m的最小值M .
(3)对于(2)中的M,正数a,b满足![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
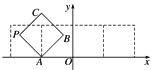
【题目】如图所示,放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:
有下列判断:
①若![]() ,则函数
,则函数![]() 是偶函数;
是偶函数;
②对任意的![]() ,都有
,都有![]() ;
;
③函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
其中判断正确的序号是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上的动点,动点
上的动点,动点![]() 满足
满足![]() (
(![]() 且
且![]() ),
),![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)在以坐标原点为极点,以![]() 轴的正半轴为极轴的极坐标系中,
轴的正半轴为极轴的极坐标系中, ![]() 点的极坐标为
点的极坐标为![]() ,射线
,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,已知
,已知![]() 面积的最大值为
面积的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.

求证:(1)CD⊥PD;(2)EF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增进市民的环保意识,某市有关部门面向全体市民进行了一次环保知识的微信问卷测试活动,每位市民仅有一次参与问卷测试机会.通过抽样,得到参与问卷测试的1000人的得分数据,制成频率分布直方图如图所示.

(1)估计成绩得分落在[86,100]中的概率.
(2)设这1000人得分的样本平均值为![]() .
.
(i)求![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(ii)有关部门为参与此次活动的市民赠送20元或10元的随机话费,每次获赠20元或10元的随机话费的概率分别为![]() 和
和![]() .得分不低于
.得分不低于![]() 的可获赠2次随机话费,得分低于
的可获赠2次随机话费,得分低于![]() 的可获赠1次随机话费.求一位市民参与这次活动获赠话费
的可获赠1次随机话费.求一位市民参与这次活动获赠话费![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com