
【题目】通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
经计算![]() 的观测值
的观测值![]() . 参照附表,得到的正确结论是
. 参照附表,得到的正确结论是
附表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ ![]() 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣ ![]() .
. 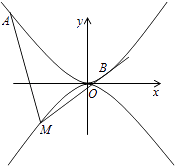
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2 ![]()
(1)求数列{an}的通项公式an;
(2)令b ![]() ,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有
,数列{bn}的前n项和为Tn . 证明:对于任意n∈N* , 都有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.
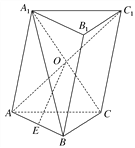
(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的是__________.
①将一组数据中的每个数据都加上或减去同一个常数后,方差不变;
②在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“若某人吸烟,则他有99%的可能患肺病;”
③已知“![]() ”为真命题,则“
”为真命题,则“![]() ”、“
”、“![]() ”、“
”、“![]() ”中至少有一个真命题;
”中至少有一个真命题;
④以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,其变换后得到线性回归方程
,其变换后得到线性回归方程![]() 则
则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 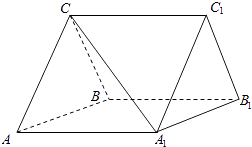
(1)证明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com