
【题目】已知函数f(x)=cos2x+2sin2x+2sinx.
(Ⅰ)将函数f(2x)的图象向右平移 ![]() 个单位得到函数g(x)的图象,若x∈[
个单位得到函数g(x)的图象,若x∈[ ![]() ,
, ![]() ],求函数g(x)的值域;
],求函数g(x)的值域;
(Ⅱ)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)= ![]() +1,A∈(0,
+1,A∈(0, ![]() ),a=2
),a=2 ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
【答案】解:(Ⅰ)因为f(x)=cos2x+2sin2x+2sinx=cosx2﹣sinx2+2sin2x+2sinx=cosx2+sinx2+2sinx=1+2sinx,
即f(2x)=1+2sin2x,
∵函数f(2x)的图象向右平移 ![]() 个单位得到函数g(x)的图象,
个单位得到函数g(x)的图象,
∴ ![]() ,∵
,∵ ![]() ,∴2x﹣
,∴2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
], ![]() ,∴g(x)∈[0,3],
,∴g(x)∈[0,3],
所以函数g(x)的值域为[0,3].
(Ⅱ)解:∵ ![]() ,∴
,∴ ![]() ;因为
;因为 ![]() ,∴
,∴ ![]() .
.
又 ![]() ,
, ![]() ,b=2,∴c=4.
,b=2,∴c=4.
所以,△ABC面积 ![]()
【解析】(Ⅰ)利用三角恒等变换化简函数f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,利用正弦函数的定义域和值域,求得数g(x)的值域.(Ⅱ)先求得cosA的值,利用余弦定理求得c的值,可得△ABC的面积.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换和余弦定理的定义对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象;余弦定理:
的图象;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点 .
.
(1)求椭圆的方程;
(2)设椭圆与![]() 轴的非负半轴交于点
轴的非负半轴交于点![]() ,过点
,过点![]() 作互相垂直的两条直线,分别交椭圆于
作互相垂直的两条直线,分别交椭圆于![]() 两点,连接
两点,连接![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 的离心率为
的离心率为![]() ,其右焦点到椭圆C外一点
,其右焦点到椭圆C外一点![]() 的距离为
的距离为![]() ,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
![]() 1
1![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 2
2![]() 求
求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 通项公式为 ![]() .
.
(Ⅰ)计算f(1),f(2),f(3)的值;
(Ⅱ)比较f(n)与1的大小,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
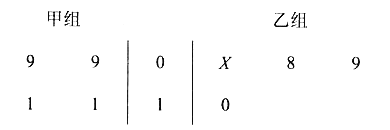
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
(Ⅰ)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(Ⅱ)在线段CD上是否存在一点E,使得直线AE与平面ADM所成角的正弦值为 ![]() ,若存在,请说明点E的位置;若不存在,请说明理由;
,若存在,请说明点E的位置;若不存在,请说明理由;
(Ⅲ)求二面角A﹣MD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心坐标![]() 且与线y=3x+4相切,
且与线y=3x+4相切,
(1)求圆C的方程;
(2)设直线![]() 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x﹣m|﹣1.
(1)若不等式f(x)≤2的解集为{x|﹣1≤x≤5},求实数m的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥t﹣2对一切实数x恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>0,b>0)的短轴长为2
(a>0,b>0)的短轴长为2![]() , 且离心率e=
, 且离心率e=![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设F1、F2是椭圆的左、右焦点,过F2的直线与椭圆相交于P、Q两点,求△F1PQ面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com