
函数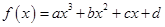 的图象(如图),则函数
的图象(如图),则函数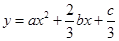 的单调递增区间是( )
的单调递增区间是( )

A.  B.
B.
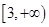
C. 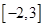 D.
D.
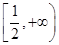
D
【解析】
试题分析:因为函数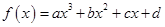 ,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=-
,则f'(x)=3ax2+2bx+c,由图可知f'(-2)=0,f'(3)=0,∴12a-4b+c=0,27a+6b+c=0,∴b=-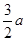 ,c=-18a,所以
,c=-18a,所以 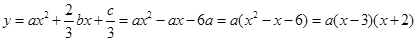 ,则y’=a(2x-1)
,则y’=a(2x-1)
∴y=3ax2-3ax-18a,结合图像可知a>0,那么y'=a(2x-1),当x> 时,y'>0,∴y=x2-x-6的单调递增区间为:[
时,y'>0,∴y=x2-x-6的单调递增区间为:[ ,+∞),故选D.
,+∞),故选D.
考点:本试题主要考查了函数极值点和单调性与函数的导数之间的关系.属基础题.
点评:解决该试题的关键是通过图像确定出-2和3为函数的极值点,那么导数值为零,从而得到a,b,c,的关系式进而化简函数,求解导数得到单调区间。


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2015届浙江省宁波市高一上学期期末考试数学试卷(解析版) 题型:选择题
函数 的图象为如图所示的折线段
的图象为如图所示的折线段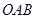 ,其中点
,其中点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .定义函数
.定义函数 ,则函数
,则函数 的最大值为
的最大值为
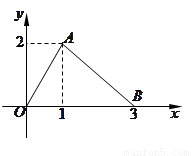
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com