Question

【题目】已知全集为R，函数f（x）= 的定义域为集合A，集合B={x|x（x﹣1）≥2}
（1）求A∩B；
（2）若C={x|1﹣m＜x≤m}，C（RB），求实数m的取值范围．

Answer 1

【答案】
（1）解：由 x﹣1＞0得，函数 f（x）的定义域A={x|x＞1}，又x2﹣x﹣2≥0，得B={x|x≥2或x≤﹣1}，

∴A∩B={x|x≥2}

（2）解：∵C{x|﹣1＜x＜2}，

①当 C=时，满足要求，此时1﹣m≥m，得 ；

②当 C≠时，要C{x|﹣1＜x＜2}，则 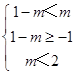，解得 ，

由①②得，m＜2，

∴实数m的取值范围（﹣∞，2）

【解析】先化简A，B，（1）根据交，并集的定义即可求出，（2）由C（RB），分类讨论，即可求出参数m的取值范围．
【考点精析】掌握集合的交集运算是解答本题的根本，需要知道交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．