
【题目】某学校有体育特长生25人,美术特长生35人,音乐特长生40人.用分层抽样的方法从中抽取40人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A.8,14,18
B.9,13,18
C.10,14,16
D.9,14,17
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
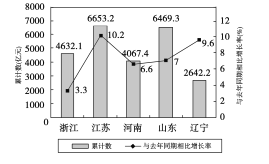
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
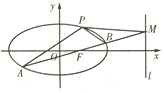
【题目】如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]()
![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() ,
, ![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,
, ![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是公差不为0的等差数列{an}的前n项和,且S1 , S2 , S4成等比数列,a5=9.
(1)求数列{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}满足:a1=3,(2n﹣1)an+2=(2n+1)an﹣1+8n2(n>1,n∈N*),设 ![]() ,数列{bn}的前n项的和Sn , 则Sn的取值范围为( )
,数列{bn}的前n项的和Sn , 则Sn的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中程序是计算2+3+4+5+6的值的程序.在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是( )
A.①i>1②i=i﹣1
B.①i>1②i=i+1
C.①i>=1②i=i+1
D.①i>=1②i=i﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com