
【题目】已知函数![]() ,
,![]() .
.
(1)设![]() ,求
,求![]() 的最小值;
的最小值;
(2)证明:当![]() 时,总存在两条直线与曲线
时,总存在两条直线与曲线![]() 与
与![]() 都相切.
都相切.
【答案】(1) x=-1时,F(x)取得最小值F(-1)=-![]() (2) 见解析
(2) 见解析
【解析】试题分析:(1)对函数求导,研究函数的单调性,得到最小值;(2)根据公切线的定义得到(t-1)et-1-t+a=0有两个根即可,研究这个函数的单调性和图像,得到这个图像和x轴有两个交点.
解析:
(Ⅰ)F(x)=(x+1)ex-1,
当x<-1时,F(x)<0,F(x)单调递减;
当x>-1时,F(x)>0,F(x)单调递增,
故x=-1时,F(x)取得最小值F(-1)=-![]() .
.
(Ⅱ)因为f(x)=ex-1,
所以f(x)=ex-1在点(t,et-1)处的切线为y=et-1x+(1-t)et-1;
因为g(x)=![]() ,
,
所以g(x)=lnx+a在点(m,lnm+a)处的切线为y=![]() x+lnm+a-1,
x+lnm+a-1,
由题意可得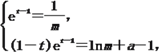 则(t-1)et-1-t+a=0.
则(t-1)et-1-t+a=0.
令h(t)=(t-1)et-1-t+a,则h(t)=tet-1-1
由(Ⅰ)得t<-1时,h(t)单调递减,且h(t)<0;
当t>-1时,h(t)单调递增,又h(1)=0,t<1时,h(t)<0,
所以,当t<1时,h(t)<0,h(t)单调递减;
当t>1时,h(t)>0,h(t)单调递增.
由(Ⅰ)得h(a-1)=(a-2)ea-2+1≥-![]() +1>0,
+1>0,
又h(3-a)=(2-a)e2-a+2a-3>(2-a)(3-a)+2a-3=(a-![]() )2+
)2+![]() >0,
>0,
h(1)=a-1<0,所以函数y=h(t)在(a-1,1)和(1,3-a)内各有一个零点,
故当a<1时,存在两条直线与曲线f(x)与g(x)都相切.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )
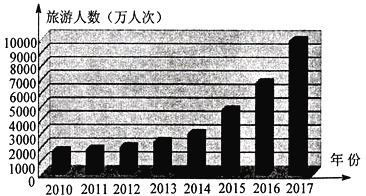
A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐代卖店代售多种类型的快餐,深受广大消费者喜爱.其中,![]() 种类型的快餐每份进价为
种类型的快餐每份进价为![]() 元,并以每份
元,并以每份![]() 元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以
元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以![]() 元的价格作特价处理,且全部售完.
元的价格作特价处理,且全部售完.
(1)若该代卖店每天定制![]() 份
份![]() 种类型快餐,求
种类型快餐,求![]() 种类型快餐当天的利润
种类型快餐当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(2)该代卖店记录了一个月![]() 天的
天的![]() 种类型快餐日需求量(每天20:00之前销售数量)
种类型快餐日需求量(每天20:00之前销售数量)
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
(i)假设代卖店在这一个月内每天定制![]() 份
份![]() 种类型快餐,求这一个月
种类型快餐,求这一个月![]() 种类型快餐的日利润(单位:元)的平均数(精确到
种类型快餐的日利润(单位:元)的平均数(精确到![]() );
);
(ii)若代卖店每天定制![]() 份
份![]() 种类型快餐,以
种类型快餐,以![]() 天记录的日需求量的频率作为日需求量发生的概率,求
天记录的日需求量的频率作为日需求量发生的概率,求![]() 种类型快餐当天的利润不少于
种类型快餐当天的利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() . 若曲线y=
. 若曲线y=![]() 在点P(e,f(e))处的切线方程为y=2x-e(为自然对数的底数).
在点P(e,f(e))处的切线方程为y=2x-e(为自然对数的底数).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,试比较
,试比较![]() 与
与![]() 的大小,并予以证明.
的大小,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地一商场记录了![]() 月份某
月份某![]() 天当中某商品的销售量
天当中某商品的销售量![]() (单位:
(单位:![]() )与该地当日最高气温
)与该地当日最高气温![]() (单位:
(单位:![]() )的相关数据,如下表:
)的相关数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)试求![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月某日的最高气温是
月某日的最高气温是![]() ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;
(3)假定该地![]() 月份的日最高气温
月份的日最高气温![]() ,其中
,其中![]() 近似取样本平均数
近似取样本平均数![]() ,
,![]() 近似取样本方差
近似取样本方差![]() ,试求
,试求![]() .
.
附:参考公式和有关数据 ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构随机调查了![]() 岁到
岁到![]() 岁之间的
岁之间的![]() 位网上购物者的年龄分布情况,并将所得数据按照
位网上购物者的年龄分布情况,并将所得数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成
分成![]() 组,绘制成频率分布直方图(如图).
组,绘制成频率分布直方图(如图).
(1)求频率分布直方图中实数![]() 的值及这
的值及这![]() 位网上购物者中年龄在
位网上购物者中年龄在![]() 内的人数;
内的人数;
(2)现采用分层抽样的方法从参与调查的![]() 位网上购物者中随机抽取
位网上购物者中随机抽取![]() 人,再从这
人,再从这![]() 人中任选
人中任选![]() 人,设这
人,设这![]() 人中年龄在
人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com