
分析 (1)x∈[0,1],通过作差f(x)-(x2-$\frac{1}{2}$x+1)变形利用基本不等式的性质可得f(x)≥x2-$\frac{1}{2}$x+1=$(x-\frac{1}{4})^{2}+\frac{15}{16}$≥$\frac{15}{16}$.
(2)f(x)=x2+$\frac{1}{\sqrt{1+x}}$≤x+$\frac{1}{\sqrt{1+x}}$=g(x),x∈[0,1],利用导数研究函数g(x)的单调性,可得最大值,即可得出.
解答 证明:(1)x∈[0,1],
f(x)-(x2-$\frac{1}{2}$x+1)=$\frac{1}{\sqrt{1+x}}$+$\frac{1}{2}x$-1=$\frac{1}{\sqrt{1+x}}$+$\frac{x+1}{2}$-$\frac{3}{2}$=$\frac{1}{2\sqrt{1+x}}$+$\frac{1}{2\sqrt{1+x}}$+$\frac{x+1}{2}$-$\frac{3}{2}$
≥3×$\frac{1}{2}$×$\root{3}{\frac{1}{\sqrt{1+x}}•\frac{1}{\sqrt{1+x}}•(1+x)}$-$\frac{3}{2}$=0,当且仅当x=0时取等号.
∴f(x)≥x2-$\frac{1}{2}$x+1=$(x-\frac{1}{4})^{2}+\frac{15}{16}$≥$\frac{15}{16}$,当且仅当x=$\frac{1}{4}$时取后一个等号,因此f(x)$>\frac{15}{16}$.
(2)f(x)=x2+$\frac{1}{\sqrt{1+x}}$≤x+$\frac{1}{\sqrt{1+x}}$=g(x),x∈[0,1],
g′(x)=1-$\frac{1}{2(1+x)^{\frac{3}{2}}}$>0,∴函数g(x)在x∈[0,1]单调递增,
∴g(x)max=g(1)=1+$\frac{1}{\sqrt{2}}$=$\frac{2+\sqrt{2}}{2}$.
∴f(x)≤$\frac{2+\sqrt{2}}{2}$.当且仅当x=1时取等号.
综上(1)(2)可得:$\frac{15}{16}$<f(x))≤$\frac{2+\sqrt{2}}{2}$.
点评 本题考查了变形利用基本不等式的性质、利用导数研究函数的单调性最值,考查了推理能力与计算能力,属于难题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (x-3)2+(y+4)2=3 | B. | (x-3)2+(y-4)2=3 | C. | (x+3)2+(y-4)2=3 | D. | $(x+3{)^2}+(y-4{)^2}=\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
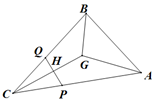 如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )
如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| B. | “x=1”是“x2-3x+2=0”的充分必要条件. | |
| C. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”是真命题 | |
| D. | 若¬(p∧q)为真命题,则p、q至少有一个为假命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
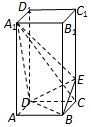 如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:
如图,在长方体ABCD-A1B1C1B1中,AA1=2AB=2AD=4,点E在CC1上且C1E=3EC.利用空间向量解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com