
【题目】如图,矩形![]() 所在的平面与正三角形
所在的平面与正三角形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
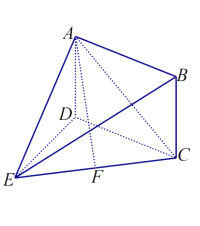
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有共同的焦点,且离心率为
有共同的焦点,且离心率为![]() ,设
,设![]() 分别是
分别是![]() 为椭圆的上下顶点
为椭圆的上下顶点
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,当弦
,当弦![]() 的中点
的中点![]() 落在四边形
落在四边形![]() 内(含边界)时,求直线
内(含边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.

(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求
的体积取最大值时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆Q经过定点![]() ,且与定直线
,且与定直线![]() 相切(其中a为常数,且
相切(其中a为常数,且![]() ).记动圆圆心Q的轨迹为曲线C.
).记动圆圆心Q的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线?
(2)设点P的坐标为![]() ,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得
,过点P作曲线C的切线,切点为A,若过点P的直线m与曲线C交于M,N两点,则是否存在直线m,使得![]() ?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线m斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏,导致一个条件看不清,具体如下:等比数列![]() 的前n项和为
的前n项和为![]() ,已知_____,
,已知_____,
(1)判断![]() ,
,![]() ,
,![]() 的关系;
的关系;
(2)若![]() ,设
,设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,证明:
,证明:![]() .
.
甲同学记得缺少的条件是首项a1的值,乙同学记得缺少的条件是公比q的值,并且他俩都记得第(1)问的答案是![]() ,
,![]() ,
,![]() 成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了50人就该城市共享单车的推行情况进行问卷调査,并将问卷中的这50人根据其满意度评分值(百分制)按照![]() 分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
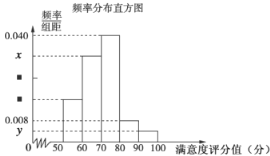
(1)求![]() 的值;
的值;
(2)若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com