
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以平面直角坐标系的原点
为参数),以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,将曲线
轴的非负半轴为极轴建立极坐标系,将曲线![]() 绕极点顺时针旋转
绕极点顺时针旋转![]() 后得到曲线的曲线记为
后得到曲线的曲线记为![]() .
.
(1)求曲线![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() 为等腰三角形,
为等腰三角形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
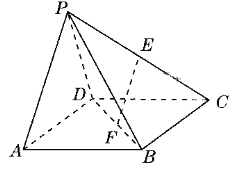
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某苗木基地常年供应多种规格的优质树苗.为更好地销售树苗,建设生态文明家乡和美好家园,基地积极主动地联系了甲、乙、丙三家公司,假定基地得到公司甲、乙、丙的购买合同的概率分别![]() 、
、![]() 、
、![]() ,且基地是否得到三家公司的购买合同是相互独立的.
,且基地是否得到三家公司的购买合同是相互独立的.
(1)若公司甲计划与基地签订300棵银杏实生苗的销售合同,每棵银杏实生苗的价格为90元,栽种后,每棵树苗当年的成活率都为0.9,对当年没有成活的树苗,第二年需再补种1棵.现公司甲为苗木基地提供了两种售后方案,
方案一:公司甲购买300棵银杏树苗后,基地需提供一年一次,共计两年的补种服务,且每次补种人工及运输费用平均为800元;
方案二:公司甲购买300棵银杏树苗后,基地一次性地多给公司甲60棵树苗,后期的移栽培育工作由公司甲自行负责.
若基地首次运送方案一的300棵树苗及方案二的360棵树苗的运费及栽种费用合计都为1600元,试估算两种方案下苗木基地的合同收益分别是多少?
(2)记![]() 为该基地得到三家公司购买合同的个数,若
为该基地得到三家公司购买合同的个数,若![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱中![]() ,它的体积是
,它的体积是![]() 底面△ABC中,∠BAC=90°,AB=4,AC=3,
底面△ABC中,∠BAC=90°,AB=4,AC=3,![]() 在底面的射影是D,且D为BC的中点.
在底面的射影是D,且D为BC的中点.

(1)求侧棱![]() 与底面ABC所成角的大小;
与底面ABC所成角的大小;
(2)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
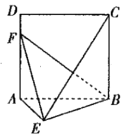
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com