
【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车![]() 辆,混合动力型公交车
辆,混合动力型公交车![]() 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加![]() ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入![]() 辆.设
辆.设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设![]() 、
、![]() 分别为
分别为![]() 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求![]() 、
、![]() ,并求
,并求![]() 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数![]() ;
;
(2)该市计划用![]() 年的时间完成全部更换,求
年的时间完成全部更换,求![]() 的最小值.
的最小值.
【答案】(1)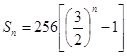 ,
,![]() ,
,![]() ;
;
(2)147.
【解析】
试题(1)设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,通过分析可知数列
年投入的电力型公交车、混合动力型公交车的数量,通过分析可知数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,数列
的等比数列,数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,由等比数列的前
的等差数列,由等比数列的前![]() 项和公式
项和公式![]() ,等差数列的前
,等差数列的前![]() 项和公式
项和公式![]() 即可求出;(2)通过分析
即可求出;(2)通过分析![]() 、
、![]() 是关于
是关于![]() 的单调递增函数,故
的单调递增函数,故![]() 是关于
是关于![]() 的单调递增函数,要求满足
的单调递增函数,要求满足![]() 的最小值应该是
的最小值应该是![]() ,此时应注意实际问题中
,此时应注意实际问题中![]() 取整的问题.
取整的问题.
试题解析:(1)设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,
年投入的电力型公交车、混合动力型公交车的数量,
依题意知,数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列; 1分
的等比数列; 1分
数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列, 2分
的等差数列, 2分
所以数列![]() 的前
的前![]() 项和
项和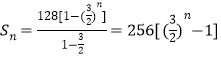 , 4分
, 4分
数列![]() 的前
的前![]() 项和
项和![]() , 6分
, 6分
所以经过![]() 年,该市更换的公交车总数
年,该市更换的公交车总数
![]() ; 7分
; 7分
(2)因为![]() 、
、![]() 是关于
是关于![]() 的单调递增函数, 9分
的单调递增函数, 9分
因此![]() 是关于
是关于![]() 的单调递增函数, 10分
的单调递增函数, 10分
所以满足![]() 的最小值应该是
的最小值应该是![]() , 11分
, 11分
即![]() ,解得
,解得![]()
![]() , 12分
, 12分
又![]() ,所以
,所以![]() 的最小值为147.
的最小值为147.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() x2﹣ax(a为常数)有两个极值点.
x2﹣ax(a为常数)有两个极值点.
(1)求实数a的取值范围;
(2)设f(x)的两个极值点分别为x1 , x2 , 若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知 ![]() ,sinA=
,sinA= ![]() . (Ⅰ)求sinC的值;
. (Ⅰ)求sinC的值;
(II)设D为AC的中点,若△ABC的面积为8 ![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若x∈[0, ![]() ],求函数f(x)的最值及相应x的取值.
],求函数f(x)的最值及相应x的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于序列A0:a0 , a1 , a2 , …,an(n∈N*),实施变换T得序列A1:a1+a2 , a2+a3 , …,an﹣1+an , 记作A1=T(A0):对A1继续实施变换T得序列A2=T(A1)=T(T(A0)),记作A2=T2(A0);…;An﹣1=Tn﹣1(A0).最后得到的序列An﹣1只有一个数,记作S(A0). (Ⅰ)若序列A0为1,2,3,求S(A0);
(Ⅱ)若序列A0为1,2,…,n,求S(A0);
(Ⅲ)若序列A和B完全一样,则称序列A与B相等,记作A=B,若序列B为序列A0:1,2,…,n的一个排列,请问:B=A0是S(B)=S(A0)的什么条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.得到甲、乙两位学生成绩的茎叶图.
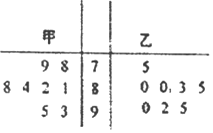
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项中,奇数项的和为56,偶数项的和为48,且
项中,奇数项的和为56,偶数项的和为48,且![]() (其中
(其中![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,…,
,…,![]() ,…是一个等比数列,其中
,…是一个等比数列,其中![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若存在实数![]() ,
,![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com