
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
【答案】C
【解析】
通过“垂直于同一直线的两条直线的位置关系不确定”可判断A是否正确;通过“底面各边相等,侧面都是矩形的四棱柱底面不一定是正方形”可判断B是否正确;通过“两条异面直线的公垂线是唯一的,所以经过空间任一点与两条异面直线都垂直的直线有且只有一条”可判断C是否正确;通过“经过球面上任意两点的大圆有无数个”可判断D是否正确。
A项:垂直于同一直线的两条直线不一定互相平行,故A错;
B项:底面各边相等,侧面都是矩形的四棱柱是直四棱柱,不一定是正四棱柱,故B错;
C项:两条异面直线的公垂线是唯一的,所以经过空间任一点与两条异面直线都垂直的直线有且只有一条,故C正确;
D项:过球面上任意两点的大圆有无数个,故D错,故选C项。


科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按照
)进行统计,按照![]()
![]() 的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在
的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在![]() 的数据).
的数据).
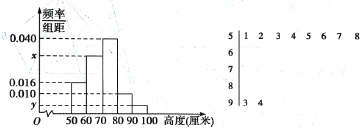
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从高度在![]() 厘米以上(含
厘米以上(含![]() 厘米)的植株中随机抽取
厘米)的植株中随机抽取![]() 株,求所取的
株,求所取的![]() 株中至少有一株高度在
株中至少有一株高度在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的序号是: _________
①已知![]() 恒成立,若
恒成立,若![]() 为真命题,则实数
为真命题,则实数![]() 的最大值为2;
的最大值为2;
②已知三点![]() 共线,则
共线,则![]() 的最小值为11;
的最小值为11;
③已知![]() 是椭圆
是椭圆![]() 的为两个焦点,点
的为两个焦点,点![]() 在椭圆
在椭圆![]() 上,则使三角形
上,则使三角形![]() 为直角三角形的点
为直角三角形的点![]() 个数4 个;
个数4 个;
④在圆![]() 内,过点
内,过点![]() 有
有![]() 条弦的长度成等差数列,最小弦长为数列的首项
条弦的长度成等差数列,最小弦长为数列的首项![]() ,最大弦长为
,最大弦长为![]() ,若公差
,若公差![]() 那么
那么![]() 的取值集合为
的取值集合为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() +
+![]() =1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=
=1(a>b>0)的短轴两端点为B1(0,﹣1)、B2(0,1),离心率e=![]() ,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,

(1)求椭圆![]() 的方程和
的方程和![]() 的值;
的值;
(2)若点![]() 坐标为(1,0),过
坐标为(1,0),过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试求
两点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有四个命题:
①函数y=tan x在每一个周期内都是增函数.
②函数y=sin(2x+ ![]() )的图象关于直线x=
)的图象关于直线x= ![]() 对称;
对称;
③函数y=tanx的对称中心(kπ,0),k∈Z.
④函数y=sin(2x﹣ ![]() )是偶函数.
)是偶函数.
其中正确结论个数( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com