练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若a>0使不等式|x-4|+|x-3|<a在R上的解集不是空集，则a的取值范围是

    A. (0，1)          B. (0，1]            C. (1，+∞)           D. [1，+∞)

    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知二次函数．

    （1）若a>b>c，　且f（1）=0，证明f（x）的图象与x轴有2个交点；

    （2）在（1）的条件下，是否存在m∈R，使池f（m）=－ a成立时，f（m+3）为正数，若存在，证明你的结论，若不存在，说明理由；

    （3）若 对，方程有2个不等实根，．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年方城一高高三年级10月月考数学试卷（理科） 题型：解答题

    （本题满分14分）已知二次函数．

    （1）若a>b>c，　且f（1）=0，证明f（x）的图象与x轴有2个交点；

    （2）若 对，方程有2个不等实根，；

    （3）在（1）的条件下，是否存在m∈R，使f（m）=－ a成立时，f（m+3）为正数，若

    存在，证明你的结论，若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年方城一高高三年级10月月考数学试卷（理科） 题型：解答题

    （本题满分14分）已知二次函数．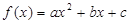

    （1）若a>b>c，　且f（1）=0，证明f（x）的图象与x轴有2个交点；

    （2）若 对，方程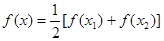有2个不等实根，；

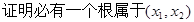    （3）在（1）的条件下，是否存在m∈R，使f（m）=－ a成立时，f（m+3）为正数，若

    存在，证明你的结论，若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f（x）=ax2+bx+c。

       （1）若a>b>c,且f（1）=0,证明f（x）的图象与x轴有两个交点;

       （2）在（1）的条件下,是否存在mR,使得当f（m）=-a成立时,f（m+3）为正数,证明你的结论;若不存在,说明理由;

       （3）若对x1,x2R,且x1<x2,f（x1）≠f（x2）,方程f（x）=[f（x1）+f（x2）]有两个不等的实根,证明必有一个实根属于（x1,x2）;

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f(x)=ax2+bx+c(a≠0).

    (1)若a>b>c,且f(1)=0,是否存在m∈R,使得f(m)=-a成立时,f(m+3)为正数?若存在,证明你的结论;若不存在,说明理由.

    (2)若对x1,x2∈R,且x1<x2,f(x1)≠f(x2),方程f(x)=[f(x1)+f(x2)]有2个不等实根,证明必有一个根属于(x1,x2).

    (3)若f(0)=0,是否存在b的值使{x|f(x)=x}={x|f(f(x))=x}成立?若存在,求出b的取值范围;若不存在,说明理由.

    查看答案和解析>>

    同步练习册答案