
【题目】已知在四棱锥![]() 中,
中,![]() ,
,![]() ,E为PC的中点,
,E为PC的中点,![]() ,
,![]()

(1)求证:![]()
(2)若![]() 与面ABCD所成角为
与面ABCD所成角为![]() ,P在面ABCD射影为O,问是否在BC上存在一点F,使面
,P在面ABCD射影为O,问是否在BC上存在一点F,使面![]() 与面PAB所成的角为
与面PAB所成的角为![]() ,若存在,试求点F的位置,不存在,请说明理由.
,若存在,试求点F的位置,不存在,请说明理由.
【答案】(1)见解析 (2)当F为BC的中点时,两平面所成的角为![]() .
.
【解析】
(1)连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 为平行四边形,得到
为平行四边形,得到![]() ,根据线面垂直判定定理即可得结论;(2)作
,根据线面垂直判定定理即可得结论;(2)作![]() ,结合可知
,结合可知![]() 为
为![]() 点在面
点在面![]() 的射影,
的射影,![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,求出面
,求出面![]() 和面
和面![]() 分别为
分别为![]() 和
和![]() ,结合夹角为
,结合夹角为![]() ,求出
,求出![]() 即可.
即可.
(1)证明:

连接BE,取PD的中点H,连接AH,则![]() 又
又![]() ,
,![]()
可知![]() 且
且![]() ,可知ABEH为平行四边形,故
,可知ABEH为平行四边形,故![]() ,所以
,所以![]() .
.
(2)![]() 面
面![]()
![]() 面
面![]() ,
,![]() ,作
,作![]() ,可知
,可知![]() 为
为![]() 点在面
点在面![]() 的射影,
的射影,![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设面POF的法向量为![]() ,
,![]() ,可知
,可知![]() ,可知
,可知![]() ,可知
,可知
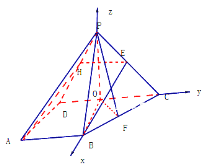
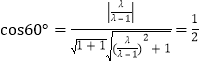 ,解得
,解得![]() ,可知当F为BC的中点时,两平面所成的角为
,可知当F为BC的中点时,两平面所成的角为![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】幻彩摩天轮位于中山市西区兴中广场C段4层高的建筑之上,与中山市第一家四星级酒店——富华酒店隔河相望,其外观是参考世界最高的摩天轮新加坡“飞行者”的设计,轮体上有36个吊舱,共可同时承载288人从高空俯瞰岐江一河两岸的美景.幻彩摩天轮直径为83m,每20min转一圈,最高点离地108m,摩天轮上的点P的起始位置在最低点处.已知在时刻t(min)时P距离地面的高度![]() ,(其中
,(其中![]() ),
),
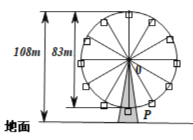
(1)求![]() 的函数解析式.
的函数解析式.
(2)当离地面![]() m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com