
����Ŀ����Ʒ�۸�����Ʒ�������Ǿ���ѧ�е�һ�ֻ�����ϵ��ij��װ��˾��������е�һ���װ�ƶ������ļ۸���Ҫ�˽��װ�ĵ���x����λ��Ԫ����������y����λ��������������z����λ��Ԫ����Ӱ�죬������10���µļ۸�![]() ����������
����������![]() ��
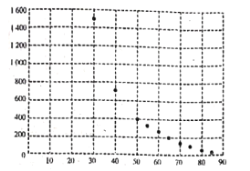
��![]() ���������˳����������õ���ͼ��ʾ��ɢ��ͼ��һЩͳ������ֵ.
���������˳����������õ���ͼ��ʾ��ɢ��ͼ��һЩͳ������ֵ.
x |
| y |
|
|
|
|
61 | 0.018 | 372 |
| 2670 | 26 | 0.0004 |
����![]() .
.
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ������y���ڼ۸�x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��һ��������Ϊ������y���ڼ۸�x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ�����������ݣ�����y����x�Ļع鷽�̣�
��3����֪������װ�ijɱ�Ϊÿ��10Ԫ�����ݣ�1���Ľ���ش��������⣻
��i��Ԥ���װ�۸�![]() ʱ������������Ԥ��ֵ�Ƕ��٣�
ʱ������������Ԥ��ֵ�Ƕ��٣�
��span>ii������װ�۸�xΪ��ֵʱ���������Ԥ��ֵ����ο�����![]() ��
��
��������һ�����ݣ���ع�ֱ�ߵ�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ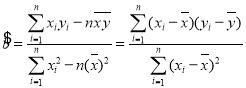 .
.
���𰸡���1��![]() ����2��
����2��![]() ����3����i��502����ii������װ�۸�
����3����i��502����ii������װ�۸�![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.
��������
��1������ɢ��ͼ����Ϻ���ͼ���������жϣ�
��2�����ݲο����ݣ��Ƚ���y��w�����Իع鷽�̣��ٽ���ת��Ϊ![]() ��
��![]() ֮��ĺ������ɣ�
֮��ĺ������ɣ�
��3�����������ݣ�2��������ع鷽�̣����ɴ�ֵ��⣻
���������ݣ�2�������������ļ��㣬���þ�ֵ����ʽ�������.
��1����ɢ��ͼ�����жϣ�![]() ��Ϊ������
��Ϊ������![]() ���ڼ۸�
���ڼ۸�![]() �Ļع鷽������.
�Ļع鷽������.
��2����![]() �Ƚ���
�Ƚ���![]() ��
��![]() �����Իع鷽�̣�
�����Իع鷽�̣�
����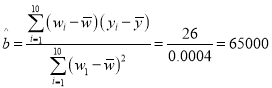
![]() ��
��
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
���![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() .
.
��3���������ɣ�2����֪���۸�![]() ʱ��
ʱ��
�����ۼ�![]() ��Ԥ��ֵΪ
��Ԥ��ֵΪ![]() .
.
�������ɣ�2����֪�������Ԥ��ֵΪ![]() ��
��
���Ե�![]() ����
����![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
�ʵ���װ�۸�![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ��
��![]() ����
����![]() �ĵ������䣻
�ĵ������䣻
![]() �Ƿ����ʵ��a��ʹ
�Ƿ����ʵ��a��ʹ![]() ����СֵΪ0�������ڣ����a��ֵ���������ڣ�˵�����ɣ�
����СֵΪ0�������ڣ����a��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���![]() Ϊ����,
����, ![]() ,
,![]() Ϊ
Ϊ![]() ���е�,��
���е�,��![]() ��
��![]() ����,�õ�����
����,�õ�����![]() ,��
,��![]() ���е�Ϊ
���е�Ϊ![]() ,�ڷ��۹�����,�õ���������������:
,�ڷ��۹�����,�õ���������������:
��![]() ƽ��
ƽ��![]() ����
����![]() �ij���Ϊ��ֵ
�ij���Ϊ��ֵ![]() ��
��
������![]() ��������Ϊ
��������Ϊ![]() ��
��
���ڷ��۹����У�����ij��λ�ã�ʹ��![]() .
.
������ȷ��������Ϊ__________����д��������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2��������![]() ��������㣬��
��������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �������ǵ�б��֮��Ϊ
�������ǵ�б��֮��Ϊ![]() ���Ƕ���
���Ƕ���![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ��
��
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��������
��ֱ��������![]() ����
����![]() ��
��![]() ���㣬�Ƿ���ڶ���
���㣬�Ƿ���ڶ���![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��
��![]() б��֮��Ϊ��ֵ�������ڣ����
б��֮��Ϊ��ֵ�������ڣ����![]() ���ꣻ�������ڣ���˵�����ɡ�
���ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�ֱ��l�IJ�������Ϊ
�У�ֱ��l�IJ�������Ϊ![]() ��tΪ����).������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��
��tΪ����).������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��![]() .
.
(1)��ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
(2)��ֱ��l������C����A��B���㣬![]() Ϊֱ��l��һ�㣬��
Ϊֱ��l��һ�㣬��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��Բ�ķ���Ϊ��
�У���֪��Բ�ķ���Ϊ��![]() ������
������![]() ����Բ�ϣ�
����Բ�ϣ�![]() Ϊԭ�㣬�߶�
Ϊԭ�㣬�߶�![]() ���е�Ϊ
���е�Ϊ![]() .
.
��1����![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵ�����
���������Ϊ���ᣬ����������ϵ�����![]() �Ĺ켣�ļ����귽�̣�
�Ĺ켣�ļ����귽�̣�
��2����ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ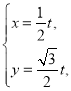 ��
��![]() ��������
��������![]() ���
���![]() �Ĺ켣����
�Ĺ켣����![]() ��
��![]() ���㣬���ҳ�
���㣬���ҳ�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������14�֣���֪��ԭ��Ķ�ֱ��![]() ��Բ
��Բ![]()
![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ��
��![]() ��
��
��1����Բ![]() ��Բ�����ꣻ
��Բ�����ꣻ
��2�����߶�![]() ���е�
���е�![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��3���Ƿ����ʵ��![]() ��ʹ��ֱ��
��ʹ��ֱ��![]()
![]() ������
������![]() ֻ��һ�����㣿�����ڣ����
ֻ��һ�����㣿�����ڣ����![]() ��ȡֵ��Χ���������ڣ�˵�����ɣ�
��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������S��ABC�У�SA��SB��SC����ABC��90����AB��BC��E��F��G�ֱ���AB��BC��CA���е㣬��ֱ��SE��SF���ɵĽ�Ϊ����ֱ��SG��ƽ��SAB���ɵĽ�Ϊ����ƽ��SEG��ƽ��SBC���ɵ�������Ϊ������ ��
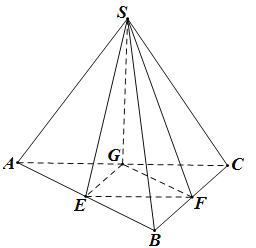
A.����������B.����������C.����������D.����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com