
【题目】已知函数f(x)=x3+ ![]() ,x∈[0,1].
,x∈[0,1].
(1)用分析法证明:f(x)≥1﹣x+x2;
(2)证明:f(x)≤ ![]() .
.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知A(-1,1),B(1,1),C(2, ![]() +1),
+1),
(1)求直线AB和AC的斜率.
(2)若点D在线段AB(包括端点)上移动时,求直线CD的斜率的变化范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体 ![]() 中,
中, ![]() 分别为
分别为 ![]() 的中点.
的中点.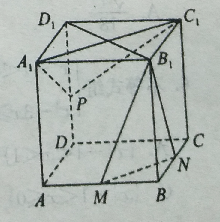
(1)求证:平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(2)当点 ![]() 在
在 ![]() 上运动时,是否都有
上运动时,是否都有 ![]() 平面
平面 ![]() ,证明你的结论;
,证明你的结论;
(3)若 ![]() 是
是 ![]() 的中点,试判断
的中点,试判断 ![]() 与平面
与平面 ![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x0 , y0)在x2+y2=r2(r>0)外,则直线x0x+y0y=r2与圆x2+y2=r2的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离三种情况均有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A,B重合),点D,E分别是A在PC,PB上的射影,则( )
A.∠ACD是二面角A﹣PC﹣B的平面角
B.∠AED是二面角A﹣PB﹣C的平面角
C.∠EDA是二面角A﹣PC﹣B的平面角
D.∠DAE是二面角B﹣PA﹣C的平面角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,a1=1,Sn=2Sn﹣1+n﹣2(n≥2),则a2017等于( )
A.22016﹣1
B.22016+1
C.22017﹣1
D.22017+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com