
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
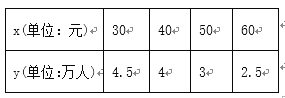
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: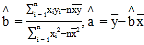
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且f(x+2)=f(x﹣2);当0≤x≤1时,f(x)= ![]() ,则f(1)+f(2)+f(3)+…+f等于( )
,则f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期“共享单车”在全国多个城市持续升温,某移动互联网机构通过对使用者的调查得出,现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示:
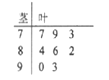
(Ⅰ)求出这组数据的平均数和中位数;
(Ⅱ)某用户从满意度指数超过80的品牌中随机选择两个品牌使用,求所选两个品牌的满意度指数均超过85的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的一个焦点与抛物线
的一个焦点与抛物线 ![]() 的焦点
的焦点 ![]() 重合,且点
重合,且点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,
, ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() .
.
(1)求椭圆 ![]() 的方程及点
的方程及点 ![]() 的坐标;
的坐标;
(2)过点 ![]() 的直线
的直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆 ![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的 ![]() 倍,得到曲线C.
倍,得到曲线C.
(1)求出C的普通方程;
(2)设直线l:x+2y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系, 求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1平面ABCD),若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( ) 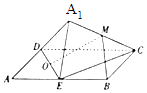
A.与平面A1DE垂直的直线必与直线BM垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置,使DE⊥MO
D.三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图. 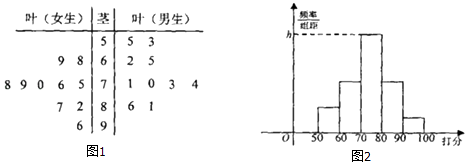
(Ⅰ)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(Ⅱ)如图2按照打分区间[0,60)、[60,70)、[70,80)、[80,90)、[90,100]绘制的直方图中,求最高矩形的高;
(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com