
| A�� | �����ε����� | B�� | �����ε����� | C�� | �����ε����� | D�� | �����εĴ��� |
���� �����������ɵó�$\overrightarrow{OB}��\overrightarrow{CA}��\overrightarrow{OC}��\overrightarrow{AB}��\overrightarrow{OA}��\overrightarrow{CB}$���Ӷ��ó�O��Ϊ��ABC�Ĵ��ģ�
��� �⣺��$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}$��
��$\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OB}•\overrightarrow{OC}$
=$\overrightarrow{OB}•��\overrightarrow{OA}-\overrightarrow{OC}��$
=$\overrightarrow{OB}•\overrightarrow{CA}$
=0��
��$\overrightarrow{OB}��\overrightarrow{CA}$��
ͬ����$\overrightarrow{OC}��\overrightarrow{AB}$��$\overrightarrow{OA}��\overrightarrow{CB}$��
��O�ǡ�ABC�������ߵĽ��㣻
���O�ǡ�ABC�Ĵ��ģ�
��ѡ��D��
���� �������������������㣬���������ļ������壬������ֱ�ij�Ҫ�����������δ��ĵĶ��壮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��a��1 | B�� | 0��a��1 | C�� | a��-1��a��1 | D�� | a=��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��������ָ������g/m3�� | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| ���������ȼ� | ������ | ������ | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ |
| ���� | 20 | 40 | m | 10 | 5 |
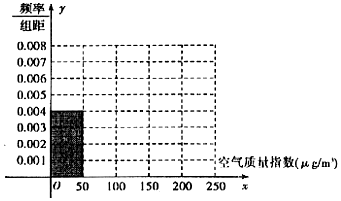
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2] | B�� | ��1��2] | C�� | [1��2] | D�� | [1��4] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4��16 | B�� | 20 | C�� | -4��20 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ�ϲ��и߶�����ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
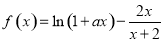 ��
��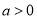 ����
����
��1����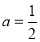 ʱ����
ʱ����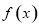 �ĵ������䣻
�ĵ������䣻
��2����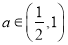 ��
��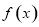 ����������ֵ��
����������ֵ��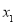 ��
��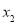 ���ԱȽ�
���ԱȽ�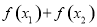 ��
��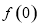 �Ĵ�С��
�Ĵ�С��
��3����֤��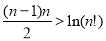 ��
��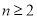 ��
��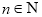 ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꼪��ʡ��һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪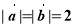 ,����
,����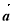 ��
��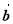 �ļн�Ϊ
�ļн�Ϊ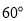 ����
����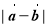 ���ڣ� ��
���ڣ� ��
A��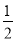 B��
B��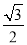 C��2 D��4
C��2 D��4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com