
【题目】已知函数f(x)= ![]() ,x∈[2,5].
,x∈[2,5].
(1)判断函数f(x)的单调性,并用定义证明你的结论;
(2)求不等式f(m+1)<f(2m﹣1)的解集.
【答案】
(1)解: ![]() ;
;
f(x)在[2,5]上单调递减,证明如下:
设x1,x2∈[2,5],且x1<x2,则:
![]() =
= ![]() ;
;
∵x1,x2∈[2,5],且x1<x2;
∴x1﹣1>0,x2﹣1>0,x2﹣x1>0;
∴f(x1)>f(x2);
∴f(x)在[2,5]上单调递减
(2)解:f(x)在[2,5]上单调递减;
∴由f(m+1)<f(2m﹣1)得:
 ;
;
解得1≤m<2;
∴原不等式的解集为[1,2)
【解析】(1)分离常数即可得到 ![]() ,容易看出f(x)在[2,5]上单调递减,根据减函数定义,设任意的x1 , x2∈[2,5],并且x1<x2 , 然后作差,通分,证明f(x1)>f(x2),从而得出f(x)的单调性;(2)根据f(x)的定义域及单调性便可由原不等式得出关于m的不等式组,解出m的范围,这样即得出原不等式的解集.
,容易看出f(x)在[2,5]上单调递减,根据减函数定义,设任意的x1 , x2∈[2,5],并且x1<x2 , 然后作差,通分,证明f(x1)>f(x2),从而得出f(x)的单调性;(2)根据f(x)的定义域及单调性便可由原不等式得出关于m的不等式组,解出m的范围,这样即得出原不等式的解集.
【考点精析】认真审题,首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性).


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知长方形![]() 中,
中,![]() ,
, ![]() 为
为![]() 的中点。将
的中点。将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() 。
。
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角![]() 的余弦值为
的余弦值为![]() 。
。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=1﹣ ![]() ,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
,g(x)=ln(ax2﹣3x+1),若对任意的x1∈[0,+∞),都存在x2∈R,使得f(x1)=g(x2)成立,则实数a的最大值为( )
A.2
B.![]()
C.4
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
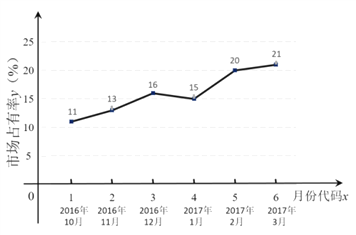
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据: ![]() ,
, ![]() .
.
参考公式:
回归直线方程为![]() 其中
其中
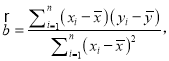
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.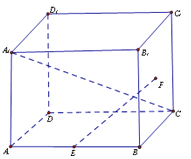
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣a(其中a∈R,e是自然对数的底数,e=2.71828…).
(Ⅰ)当a=e时,求函数f(x)的极值;
(Ⅱ)若f(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
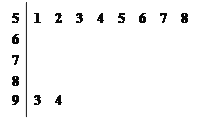
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(Ⅱ)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取3
名学生参加“中国谜语大会”,设随机变量![]() 表示所抽取的3名学生中得分在
表示所抽取的3名学生中得分在![]() 内的学生人数,求随机变量
内的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
(1)求证:AE∥l;
(2)当以AE为直径的圆过点B时,求AB的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若圆![]() 的任意一条切线
的任意一条切线![]() 与椭圆E相交于P,Q两点,试问:
与椭圆E相交于P,Q两点,试问: ![]() 是否为定值? 若是,求这个定值;若不是,说明理由.
是否为定值? 若是,求这个定值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com