
|
| a | 2 1 |
| a | 2 1 |
科目:高中数学 来源: 题型:
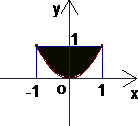 利用计算机随机模拟方法计算图中阴影面积(如图所示)
利用计算机随机模拟方法计算图中阴影面积(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:
|
| a | 2 1 |
| a | 2 1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查文科数学试卷(解析版) 题型:填空题
利用计算机随机模拟方法计算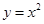 与
与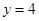 所围成的区域
所围成的区域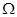 的面积时,可以先运行以下算法步骤:
的面积时,可以先运行以下算法步骤:
第一步:利用计算机产生两个在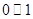 区间内的均匀随机数
区间内的均匀随机数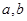 ;
;
第二步:对随机数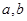 实施变换:
实施变换: 得到点
得到点
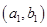 ;
;
第三步:判断点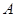
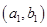 的坐标是否满足
的坐标是否满足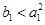 ;
;
第四步:累计所产生的点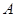 的个数
的个数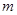 ,及满足
,及满足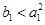 的点
的点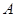 的个数
的个数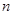 ;
;
第五步:判断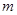 是否小于
是否小于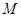 (一个设定的数).若是,则回到第一步,否则,输出
(一个设定的数).若是,则回到第一步,否则,输出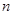 并终止算法.
并终止算法.
若设定的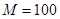 ,且输出的
,且输出的 ,则据此用随机模拟方法可以估计出区域
,则据此用随机模拟方法可以估计出区域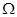 的面积为
的面积为
(保留小数点后两位数字).
查看答案和解析>>
科目:高中数学 来源:2010-2012学年广东省广州市增城中学高二(上)数学每周一测(7)(10.24)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com