
����Ŀ��ijȺ����˾�ͨ��ʱ�䣬��ָ�����ڸ�Ⱥ���г�Ա�Ӿ�ס�ص������ص�ƽ����ʱ.ij���ϰ���![]() �еij�Ա�����Լݻ���ʽͨ��.������ʾ����
�еij�Ա�����Լݻ���ʽͨ��.������ʾ����![]() ��
��![]()
![]() �ij�Ա�Լ�ʱ���Լ�Ⱥ����˾�ͨ��ʱ��Ϊ
�ij�Ա�Լ�ʱ���Լ�Ⱥ����˾�ͨ��ʱ��Ϊ ����λ�����ӣ���������Ⱥ����˾�ͨ��ʱ�䲻��
����λ�����ӣ���������Ⱥ����˾�ͨ��ʱ�䲻��![]() Ӱ�죬��Ϊ
Ӱ�죬��Ϊ![]() ���ӣ��Ը���������������ش��������⣺
���ӣ��Ը���������������ش��������⣺
��1����![]() ȡ��ֵʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣿
ȡ��ֵʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣿
��2����֪�ϰ���![]() ���˾�ͨ��ʱ����㹫ʽΪ
���˾�ͨ��ʱ����㹫ʽΪ![]() ������
������![]() �����ԣ���˵����ʵ������.
�����ԣ���˵����ʵ������.
���𰸡���1��![]() ��
��![]() ʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣻
ʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣻
��2��������
��������
��1��ȡ![]() ����ô�.
����ô�.
��2������õ� �����жϵ����Եõ���.
�����жϵ����Եõ���.
��1��������֪����![]() ʱ��
ʱ��
��![]() �������
�������![]() �����
�����![]() ��
��![]() .
.
��ˣ���![]() ��
��![]() ʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣻
ʱ������Ⱥ����˾�ͨ��ʱ������Լ�Ⱥ����˾�ͨ��ʱ�䣻
��2����![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]()
��
��![]() ʱ������
ʱ������![]() �����ݼ���
�����ݼ���
��![]() ʱ������
ʱ������![]() �����ݼ���
�����ݼ���
��![]() ʱ������
ʱ������![]() ��������.
��������.
˵���õ��ϰ���![]() ����С��
����С��![]() �����Լ�ʱ���˾�ͨ��ʱ���ǵݼ��ģ�
�����Լ�ʱ���˾�ͨ��ʱ���ǵݼ��ģ�
�д���![]() �����Լ�ʱ���˾�ͨ��ʱ���ǵ����ģ�
�����Լ�ʱ���˾�ͨ��ʱ���ǵ����ģ�
���Լ�����Ϊ![]() ʱ���˾�ͨ��ʱ������.
ʱ���˾�ͨ��ʱ������.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������PABC�У�PA������ABCD��AD��BC��AB=AD=AC=3��PA=BC=4��MΪ�߶�AD��һ�㣬AM=2MD��NΪPC���е�.

������֤��MN��ƽ��PAB;
��������ֱ��AN��ƽ��PMN���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ȫ��ѧ��Ϊ����ѧ����������һԪǮ��һƬ�ģ�������ˮ�����ѧ���ڹ�ˮ��ÿ��ȡһƿ��Ȫˮ�����Ծ�������������Ͷ��һԪǮ����ͳ��������5����۳���������������±���
�۳�ˮ��x����λ���䣩 | 7 | 6 | 6 | 5 | 6 |
����y����λ��Ԫ�� | 165 | 142 | 148 | 125 | 150 |
(��) ��x��y��������أ���ij���۳�8��ˮʱ��Ԥ������Ϊ����Ԫ��
(��) ���п����Ժ�ѧУ������������ˮ�����棬�Խ�ѧ�����ʽ������Ʒѧ���ŵ����������涨�������������꼶ǰ200������һ�Ƚ�ѧ��500Ԫ�������꼶201��500 ��������Ƚ�ѧ��300Ԫ�������꼶501���Ժ��������������ý�ѧ�𡣼ס�������ѧ����һ�Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������Ƚ�ѧ��ĸ��ʾ�Ϊ
������Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������ý�ѧ��ĸ��ʾ�Ϊ
������ý�ѧ��ĸ��ʾ�Ϊ![]() .
.
����ѧ����ý�ѧ�������£��������һ�Ƚ�ѧ��ĸ��ʣ�
����֪�ס�������ѧ������ĸ��ȵڵĽ�ѧ����������ģ���ס�������ѧ������ý�ѧ���ܽ��X �ķֲ��м���ѧ������
���� 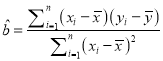 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊʵ��.
Ϊʵ��.
(1)��![]() ʱ����
ʱ����![]() ����Сֵ
����Сֵ![]() ��
��
(2)������ʵ��![]() ��ʹ�ö�����ʵ��
��ʹ�ö�����ʵ��![]() ����
����![]() ��������
��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��9�ľŸ�������ȡ����ż���ĸ����������ʣ�
������ɶ��ٸ�û���ظ����ֵ���λ����
��������λ��������ż������һ����м�����
���ڢ��е���λ���У�ż������һ������Ҳ����һ����м�����
���ڢ���������ż���������ڵ���λ���м�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y2=2px�Ľ���ΪF���߷�����x=��1��
��I����������ߵķ��̣�
���������M�ڴ��������ϣ���|MF|=3����OΪ����ԭ�㣬����OFM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ��ѡ��Ϊ�� ��
��ƽ����һ��ֱ����ƽ���ڵ�һ��ֱ��ƽ�У����ֱ�����ƽ��ƽ�У�
��һ��ƽ���ڵ�һ��ֱ������һ��ƽ��ƽ�У���������ƽ��ƽ�У�
��һ��ֱ����һ��ƽ���ڵ�����ֱ�ߴ�ֱ�����ֱ�����ƽ�洹ֱ��
��һ��ƽ�����һ��ƽ��Ĵ��ߣ���������ƽ�洹ֱ.
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ����������
����������![]() ,(
,(![]() ).
).
��1����![]() ����С�����ں���Сֵ��
����С�����ں���Сֵ��
��2���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��a=
��a=![]() ��
��![]() ����߳�
����߳�![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com