
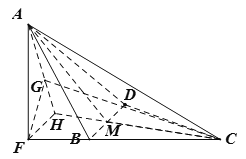
【题目】如图,在三棱锥![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 为其中心.面
为其中心.面![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.

(1)证明:![]() 面
面![]() ;
;
(2)求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:
(1)连结![]() ,由重心的性质可得在
,由重心的性质可得在![]() 中有
中有![]() ,则
,则![]() ,结合线面平行的判定定理可得
,结合线面平行的判定定理可得![]() 平面
平面![]() .
.
(2)解法一:作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,由题意可得
,由题意可得![]() 为
为![]() 与面
与面![]() 所成角,
所成角,![]() .
.
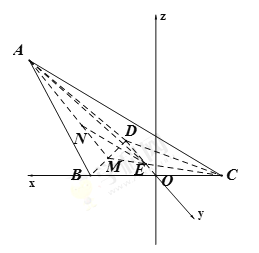
解法二:以![]() 中点为原点,建立空间直角坐标系.可得
中点为原点,建立空间直角坐标系.可得![]() ,面
,面![]() 的法向量为
的法向量为![]() ,则所求角的正弦值
,则所求角的正弦值![]() .
.
试题解析:
(1)连结![]() ,因为
,因为![]() 是正三角形
是正三角形![]() 的中心,所以
的中心,所以![]() 在
在![]() 上且
上且![]() ,又
,又![]() ,所以在
,所以在![]() 中有
中有![]() ,
,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
由面![]() 面
面![]() 知
知![]() 面
面![]() ,所以
,所以![]() ,又
,又![]()
![]() ,所以
,所以![]()
![]()
所以![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,作
,作![]() ,则
,则![]() 面
面![]()
连结![]() ,则
,则![]() 为
为![]() 与面
与面![]() 所成角,
所成角,
∴![]() ,即所求角的正弦值为
,即所求角的正弦值为![]() .
.
解法二:以![]() 中点为原点,建立如图所示的空间直角坐标系.
中点为原点,建立如图所示的空间直角坐标系.
∵![]() ,
, ![]()
∴![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]() ,则
,则
取![]() ,
,
∴![]() ,即所求角的正弦值为
,即所求角的正弦值为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中, ![]() 在线段
在线段![]() 上运动且不与
上运动且不与![]() ,
, ![]() 重合,给出下列结论:
重合,给出下列结论:
①![]() ;
;
②![]() 平面
平面![]() ;
;
③二面角![]() 的大小随
的大小随![]() 点的运动而变化;
点的运动而变化;
④三棱锥![]() 在平面
在平面![]() 上的投影的面积与在平面
上的投影的面积与在平面![]() 上的投影的面积之比随
上的投影的面积之比随![]() 点的运动而变化;
点的运动而变化;
其中正确的是( )
A. ①③④ B. ①③
C. ①②④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图, 弧AC 长为 ![]() ,弧A1B1 长为
,弧A1B1 长为 ![]() ,其中B1与C在平面AA1O1O的同侧.
,其中B1与C在平面AA1O1O的同侧. 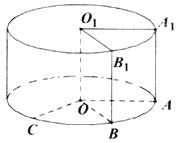
(1)求圆柱的体积与侧面积;
(2)求异面直线O1B1与OC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数X的分布列为
X | 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.Y表示经销一件该商品的利润.
(1)求事件:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(2)求Y的分布列及E(Y).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() R,函数
R,函数 ![]() =
= ![]() .
.
(1)当 ![]() 时,解不等式
时,解不等式 ![]() >1;
>1;
(2)若关于 ![]() 的方程
的方程 ![]() +
+ ![]() =0的解集中恰有一个元素,求
=0的解集中恰有一个元素,求 ![]() 的值;
的值;
(3)设 ![]() >0,若对任意
>0,若对任意 ![]()
![]() ,函数
,函数 ![]() 在区间
在区间 ![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方辑私船奉命以
处的我方辑私船奉命以![]() 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以![]() 海里/小时的速度,以
海里/小时的速度,以![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个类比中,正确的个数为
(1)若一个偶函数在R上可导,则该函数的导函数为奇函数。将此结论类比到奇函数的结论为:若一个奇函数在R上可导,则该函数的导函数为偶函数。
(2)若双曲线的焦距是实轴长的2倍,则此双曲线的离心率为2.将此结论类比到椭圆的结论为:若椭圆的焦距是实轴长的一半,则此椭圆的离心率为![]() .
.
(3)若一个等差数列的前3项和为1,则该数列的第2项为![]() .将此结论类比到等比数列的结论为:若一个等比数列的前3项积为1,则该数列的第2项为1
.将此结论类比到等比数列的结论为:若一个等比数列的前3项积为1,则该数列的第2项为1
(4)在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4.将此结论类比到空间中的结论为:在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为1:8.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com