
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求导求出![]() ,对
,对![]() 分类讨论,以
分类讨论,以![]() (或
(或![]() )是否恒成立作为分类标准,当
)是否恒成立作为分类标准,当![]() (或
(或![]() )不恒成立,求出
)不恒成立,求出![]() 的解,即可得出结论;
的解,即可得出结论;
(Ⅱ)构造函数![]() ,原问题转化为对任意的
,原问题转化为对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,利用求导方法,求出
,利用求导方法,求出![]() 的最值,将问题转化为
的最值,将问题转化为![]() 与
与![]() 的函数关系,即可求解.
的函数关系,即可求解.
(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
故函数![]() 的单增区间为
的单增区间为![]() ,无单减区间.
,无单减区间.
(2)当![]() ,即
,即![]() 时,由
时,由![]() 解得
解得
![]() 或
或![]() ,
,
i)当![]() 时,
时,![]() ,
,
所以当![]() 或
或![]() 时
时![]() ,
,
当![]() 时
时![]() .
.
ii)当![]() 时,
时,![]() ,
,
所以当![]() 时
时![]() ,
,
当![]() 时
时![]() ;
;
综上所述:
当![]() 时,函数
时,函数![]() 的单增区间为
的单增区间为![]() ,无单减区间.
,无单减区间.
当![]() 时,函数
时,函数![]() 的单增区间为
的单增区间为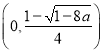 和
和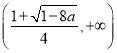 ,
,
单减区间为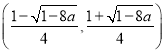 .
.
当![]() 时,函数
时,函数![]() 的单增区间为
的单增区间为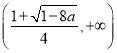 ,
,
单减区间为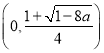 .
.
(Ⅱ)令![]() ,
,![]() .
.
原问题等价于:对任意的![]() ,总存在
,总存在![]() ,
,
使得![]() 成立,即
成立,即![]() .
.
∵![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
令![]() ,
,![]() ,只需
,只需![]() ,
,
![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】港珠澳大桥于2018年10月2刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米.桥面为双向六车道高速公路,大桥通行限速100km/h,现对大桥某路段上1000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h的频率分别为( )
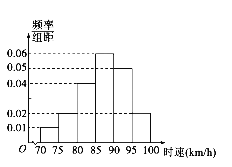
A. 300,![]() B. 300,
B. 300,![]() C. 60,
C. 60,![]() D. 60,
D. 60,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() 万元和销售额
万元和销售额![]() 万元的数据统计如下表:
万元的数据统计如下表:
城市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合y与x关系,求y关于x的线性回归方程.
(2)若用对数函数回归模型拟合y与x的关系,可得回归方程![]() ,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式: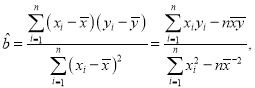
![]() ,
,
相关指数: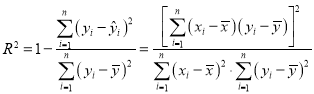 (注意:
(注意:![]() 与
与![]() 公式中的相似之处)
公式中的相似之处)
查看答案和解析>>
科目:高中数学 来源: 题型:
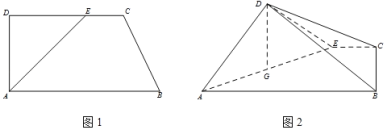
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的体积;
的体积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com