
【题目】如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图,则下列判断正确的是( )
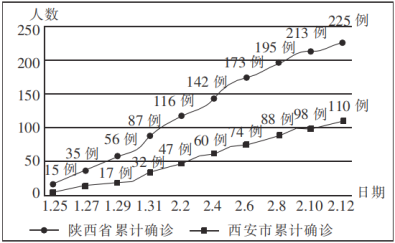
A.1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了![]()
B.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例
D.2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点F且倾斜角为
的焦点F且倾斜角为![]() 的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
(1)求抛物线C的方程;
(2)直线l交抛物线C于DE两点,且这两点位于x轴两侧,与x轴交于点M,若![]() ·
·![]() 求
求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政人民心”我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收人
收人![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税基数 | 每月应纳税所得额(含税) | 税率(%) | 每月应纳税所得额(含税) | 税率(%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
… | … | … | … | … |
随机抽取某市2020名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是![]() ;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的
;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
(1)求在旧政策下该收入层级的![]() 从业者每月应纳的个税;
从业者每月应纳的个税;
(2)设该市该收入层级的![]() 从业者2019年月缴个税为X元,求X的分布列和期望;
从业者2019年月缴个税为X元,求X的分布列和期望;
(3)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴纳的个税之和就超过2019年的人均月收入?
从业者各月少缴纳的个税之和就超过2019年的人均月收入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差![]() 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时![]() 的值.
的值.
(注:![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点S为正方形ABCD所在平面外一点,△SBC是边长为2的等边三角形,点E为线段SB的中点.
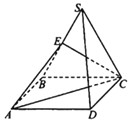
(1)证明:SD//平面AEC;
(2)若侧面SBC⊥底面ABCD,求平面ACE与平面SCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为其左顶点,点
为其左顶点,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,当
两点,当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .
.
(1)求该椭圆的方程;
(2)设直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,设直线
,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com