
已知数列 是首项
是首项 的等比数列,其前
的等比数列,其前 项和
项和 中
中 ,
, ,
, 成
成
等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,若
,若 ,求证:
,求证: .
.
(1)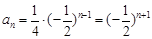 (2)见解析
(2)见解析
【解析】(1)要注意讨论q=1和 ,当q=1时,不成立;
,当q=1时,不成立;
当 时,由
时,由 ,
,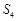 ,
, 成等差数列得可建立关于q的方程,可求出q的值.
成等差数列得可建立关于q的方程,可求出q的值.
通项公式确定.
(2)在(1)的基础上可知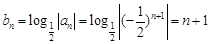 ,
,
所以 ,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.
,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.
解:(1)若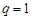 ,则
,则 显然
显然 ,
,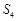 ,
, 不构成等差数列.--2分
不构成等差数列.--2分
∴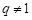 , 当
, 当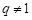 时,由
时,由 ,
,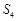 ,
, 成等差数列得
成等差数列得
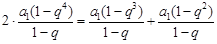
∴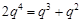
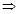
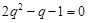
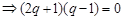 ,
,
∵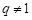 ∴
∴ -----------5分
-----------5分
∴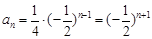 --------------6分
--------------6分
(2)∵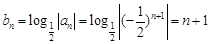
∴ ------------8分
------------8分
∴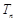 =
=
=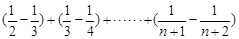
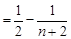 ---------11分
---------11分
 ,
,
 是递增数列.
是递增数列.
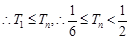 . ------------14分
. ------------14分


科目:高中数学 来源: 题型:
| ||
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南通市高三第三次调研测试数学试卷(解析版) 题型:解答题
已知数列 是首项为1,公差为
是首项为1,公差为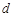 的等差数列,数列
的等差数列,数列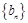 是首项为1,公比为
是首项为1,公比为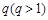 的等比
的等比
数列.
(1)若 ,
, ,求数列
,求数列 的前
的前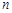 项和;
项和;
(2)若存在正整数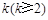 ,使得
,使得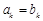 .试比较
.试比较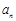 与
与 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求{an}的通项an;
(2)求使Sn>0的最大值n.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省唐山市高一(下)期中数学试卷(解析版) 题型:填空题
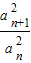 =p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com