
【题目】设 ![]() 是定义在
是定义在 ![]() 上的奇函数,且对任意实数
上的奇函数,且对任意实数 ![]() ,恒有
,恒有 ![]() .当
.当 ![]() 时,
时, ![]() .
.
(1)求证: ![]() 是周期函数;
是周期函数;
(2)当 ![]() 时,求
时,求 ![]() 的解析式;
的解析式;
(3)计算 ![]() .
.
【答案】
(1)解: ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() 是周期为
是周期为 ![]() 的周期函数.
的周期函数.
(2)解:当 ![]() 时,
时, ![]() ,由已知得
,由已知得 ![]() .
.
又 ![]() 是奇函数,
是奇函数, ![]()
![]() ,
, ![]()
![]() ,
,
又当 ![]() 时,
时, ![]() ,
, ![]()
![]() ,
,
又 ![]() 是周期为
是周期为 ![]() 的周期函数,
的周期函数,
![]()
![]() ,
,
从而求得 ![]() 时,
时, ![]() .
.
(3)解: ![]() ,又
,又 ![]() 是周期为
是周期为 ![]() 的周期函数,
的周期函数,
![]()
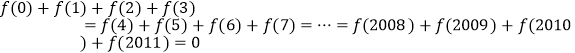 又
又 ![]() ,
,
![]()
![]() .
.
【解析】(1)根据题意利用函数的周期即可求出结果。(2)由题意结合函数的奇偶性即可求出 f ( x 4 )的解析式再放假函数的周期为4故可得到当 x ∈ [ 2 , 4 ] 时f ( x )的解析式。(3)利用函数的周期递推即可得出结果。
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线 ![]() 为参数),圆
为参数),圆 ![]() (
( ![]() 为参数),
为参数),
(Ⅰ)当 ![]() 时,求
时,求 ![]() 与
与 ![]() 的交点坐标;
的交点坐标;
(Ⅱ)过坐标原点 ![]() 作
作 ![]() 的垂线,垂足为
的垂线,垂足为 ![]() ,
, ![]() 为
为 ![]() 的中点,当
的中点,当 ![]() 变化时,求
变化时,求 ![]() 点轨迹的参数方程,并指出它是什么曲线.
点轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正弦型函数![]() 有如下性质:最大值为4,最小值为
有如下性质:最大值为4,最小值为![]() ;相邻两条对称轴间的距离为
;相邻两条对称轴间的距离为![]() .
.
(1)求函数![]() 解析式;
解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在区间
在区间![]() 上有两个不同的实根,求实数
上有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10分之间,某市级医院妇产科对1月份出生的新生儿随机抽取了16名,以下表格记录了他们的评分情况.
(1)现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率;
(2)以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿任选3名,记 ![]() 表示抽到评分不低于9分的新生儿数,求
表示抽到评分不低于9分的新生儿数,求 ![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一期间,某商场决定从 ![]() 种服装、
种服装、 ![]() 种家电、
种家电、 ![]() 种日用品中,选出
种日用品中,选出 ![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出 ![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高 ![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有 ![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为 ![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为 ![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是 ![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额 ![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com