
【题目】已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
(1)若AF=4,求点A的坐标;
(2)求线段AB的长的最小值.
【答案】(1) (3,2![]() )或(3,-2
)或(3,-2![]() ) (2)4
) (2)4
【解析】
试题(1)由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).设A![]() ,B
,B![]() .由抛物线的定义可知,
.由抛物线的定义可知,![]() ,从而
,从而![]() .由此能得到点A的坐标;(2)分类讨论,设直线l的方程为y=k(x-1),代入y2=4x整理得
.由此能得到点A的坐标;(2)分类讨论,设直线l的方程为y=k(x-1),代入y2=4x整理得![]() ,其两根为
,其两根为![]() ,且
,且![]() .由抛物线的定义可知线段AB的长
.由抛物线的定义可知线段AB的长
试题解析:(1)由抛物线的定义可知,AF=x1+![]() ,
,
从而x1=4-1=3.
代入y2=4x,解得y1=±![]() .
.
∴点A的坐标为(3,![]() )或(3,-
)或(3,-![]() ).
).
(2)当直线l的斜率存在时,
设直线l的方程为y=k(x-1).
与抛物线方程联立![]() ,
,
消去y,整理得k2x2-(2k2+4)x+k2=0,
因为直线与抛物线相交于A、B两点,
则k≠0,并设其两根为x1,x2,则![]()
由抛物线的定义可知,
![]()
当直线l的斜率不存在时,直线l的方程为x=1,与抛物线相交于A(1,2),B(1,-2),
此时AB=4,所以,AB≥4,即线段AB的长的最小值为4.


科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
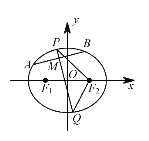
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一次围棋比赛,每局胜者得1分,负者得0分,约定一方比另一方多3分或满9局时比赛结束,并规定:只有一方比另一方多三分才算赢,其它情况算平局,假设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
(1) 求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 得分布列及数学期望.
得分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.某环保人士从当地某年的AQI记录数据中,随机抽取了15天的AQI数据,用如图所示的茎叶图记录.根据该统计数据,估计此地该年空气质量为优或良的天数约为__________.(该年为366天)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(-2,1),b=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足a·b=-1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足a·b<0的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com