
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
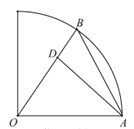
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: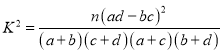
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角△![]() 中,
中,![]() ,△
,△![]() 通过△
通过△![]() 以直线
以直线![]() 为轴顺时针旋转120°得到(
为轴顺时针旋转120°得到(![]() ),点
),点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.
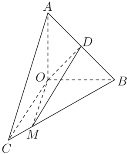
(1)求证:![]() ,并证明:
,并证明:![]() 平面
平面![]() ;
;
(2)分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(用反余弦运算表示);
所成角的大小(用反余弦运算表示);
(3)若![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的“局部对称点”.
的“局部对称点”.
(1)![]() ,其中
,其中![]() ,试判断
,试判断![]() 是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
(2)若函数![]() 在区间
在区间![]() 内有“局部对称点”,求实数m的取值范围;
内有“局部对称点”,求实数m的取值范围;
(3)若函数![]() 在R上有“局部对称点”,求实数m的取值范围.
在R上有“局部对称点”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com