
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xn,…,x2008;y1,y2,…,yn,…,y2008.
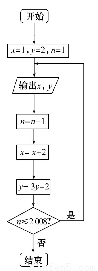
(1)求数列{xn}的通项公式.
(2)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论.
(3)求zn=x1y1+x2y2+…+xnyn(n∈N*,n≤2008).
(1) xn=2n-1(n∈N*,n≤2008)
(2) yn=3n-1(n∈N*,n≤2008),证明见解析
(3) zn=(n-1)·3n+1+3-n2(n∈N*,n≤2008)
【解析】(1)由框图,知数列{xn}中,x1=1,xn+1=xn+2,
∴xn=1+2(n-1)=2n-1(n∈N*,n≤2008).
(2)y1=2,y2=8,y3=26,y4=80.
由此,猜想yn=3n-1(n∈N*,n≤2008).
证明:由框图,知数列{yn}中,yn+1=3yn+2,
∴yn+1+1=3(yn+1),∴ =3,y1+1=3,
=3,y1+1=3,
∴数列{yn+1}是以3为首项,3为公比的等比数列,
∴yn+1=3·3n-1=3n,
∴yn=3n-1(n∈N*,n≤2008).
(3)zn=x1y1+x2y2+…+xnyn
=1×(3-1)+3×(32-1)+…+(2n-1)(3n-1)
=1×3+3×32+…+(2n-1)·3n-[1+3+…+(2n-1)]
记Sn=1×3+3×32+…+(2n-1)·3n ①
则3Sn=1×32+3×33+…+(2n-1)·3n+1 ②
①-②,得-2Sn=3+2·32+2·33+…+2·3n-(2n-1)·3n+1
=2(3+32+…+3n)-3-(2n-1)·3n+1
=2× -3-(2n-1)·3n+1
-3-(2n-1)·3n+1
=3n+1-6-(2n-1)·3n+1
=2(1-n)·3n+1-6,
∴Sn=(n-1)·3n+1+3.
又1+3+…+(2n-1)=n2,
∴zn=(n-1)·3n+1+3-n2(n∈N*,n≤2008).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
已知某物体的温度θ(单位:摄氏度)随时间t(单位:分钟)的变化规律是:θ=m·2t+21-t(t≥0,且m>0).
(1)如果m=2,求经过多少时间,物体的温度为5摄氏度.
(2)若物体的温度总不低于2摄氏度,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
已知函数f(x)=3x+x-5的零点x0∈[a,b],且b-a=1,a,b∈N*,则a+b= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
已知符号函数sgn(x)=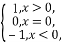 则函数f(x)=sgn(lnx)-lnx的零点个数为( )
则函数f(x)=sgn(lnx)-lnx的零点个数为( )
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十第九章第一节练习卷(解析版) 题型:选择题
如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
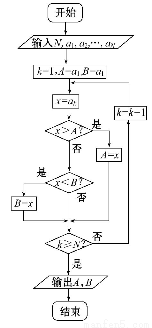
(A)A+B为a1,a2,…,aN的和
(B)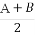 为a1,a2,…,aN的算术平均数
为a1,a2,…,aN的算术平均数
(C)A和B分别是a1,a2,…,aN中最大的数和最小的数
(D)A和B分别是a1,a2,…,aN中最小的数和最大的数
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:填空题
从集合{1,2,3,4,5,6,7,8,9,10}中选出五个数组成子集,使得这五个数中的任何两个数的和都不为11,这样的子集共有 个.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:填空题
设(x-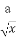 )6(a>0)的展开式中x3的系数为A,常数项为B.若B=4A,则a的值是 .
)6(a>0)的展开式中x3的系数为A,常数项为B.若B=4A,则a的值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:选择题
从甲、乙等5人中选3人排成一列,则甲不在排头的排法种数是( )
(A)12 (B)24 (C)36 (D)48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com