
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,其中
的等差中项,其中![]() 、
、![]() 、
、![]() 都是正数,过点
都是正数,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆的方程;
(2)点![]() 是椭圆上一动点,定点
是椭圆上一动点,定点![]() ,求△
,求△![]() 面积的最大值;
面积的最大值;
(3)已知定点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 相异两点.证明:对任意的
相异两点.证明:对任意的![]() ,都存在实数
,都存在实数![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由![]() 是
是![]() 与
与![]() 的等差中项得到
的等差中项得到![]() ,设出直线的方程,利用点到直线的距离公式,列出方程,求得
,设出直线的方程,利用点到直线的距离公式,列出方程,求得![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)当椭圆上的点![]() 到直线
到直线![]() 距离最大时,△
距离最大时,△![]() 面积取得最大值,设出平行直线,即可得到结论;
面积取得最大值,设出平行直线,即可得到结论;
(3)将直线的方程代入椭圆的方程,利用韦达定理及向量知识,结合判别式,即可得到结论.
(1)由![]() 是
是![]() 与
与![]() 的等差中项,可得
的等差中项,可得![]()
过点![]() 和
和![]() 的直线方程为
的直线方程为![]() ,即
,即![]() ,
,
又由该直线与原点的距离为![]() ,由点到直线的距离公式得
,由点到直线的距离公式得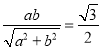
解得![]() ,所以椭圆方程为
,所以椭圆方程为![]() .
.
(2)由(1)得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且
,且![]() ,
,
当椭圆上的点![]() 到直线
到直线![]() 距离最大时,△
距离最大时,△![]() 面积取得最大值
面积取得最大值
设与直线![]() 平行的直线方程为
平行的直线方程为![]() ,
,
将其代入椭圆方程![]() ,得
,得![]() ,
,
由![]() ,解得
,解得![]() ,
,
当![]() 时,椭圆上的点
时,椭圆上的点![]() 到直线
到直线![]() 距离最大为
距离最大为![]() ,
,
此时△![]() 面积为
面积为![]() .
.
(3)将![]() 代入椭圆方程,得
代入椭圆方程,得![]() ,
,
由直线与椭圆有两个交点,所以![]() ,解得
,解得![]()
设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
因为以![]() 为直径的圆过
为直径的圆过![]() 点,所以
点,所以![]() ,即
,即![]() ,
,
而![]() ,
,
所以![]() ,解得
,解得![]() ,
,
如果![]() 对任意的
对任意的![]() 都成立,则存在
都成立,则存在![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点,
点,
又因为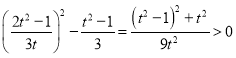 ,即
,即![]() ,
,
所以对任意的![]() ,都存在
,都存在![]() 使得以线段
使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中:①若“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②若“![]() ,
,![]() ”,则实数
”,则实数![]() 的取值范围是
的取值范围是![]() ;
;
③已知平面![]() 、
、![]() 、
、![]() ,直线
,直线![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④函数![]() 的所有零点存在区间是
的所有零点存在区间是![]() .
.
其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题一“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从点
,若将军从点![]() 处出发,河岸线所在直线方程为
处出发,河岸线所在直线方程为![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知正方形铁片![]() 边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
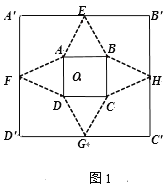
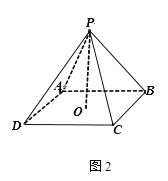
(1)若正四棱锥的棱长都相等,求所围成的正四棱锥的全面积S;
(2)请写出正四棱锥的体积V关于x的函数,并求V的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日是新中国的第70个国庆日,庄重的阅兵、欢乐的游行、热烈的联欢尽显祖国的繁荣昌盛.为了了解当天某校900名高三学生的观看情况,从中抽取了100名学生,情况如下表所示:
观看情况 | 电视观看 | 网络观看 | 没有观看 |
人数 | 35 | 60 | 5 |
新时代下,网络观看使用最多的是手机,其它还有电脑、ipad等.“是否使用手机观看”与“学生的性别”之间对应的列联表如下:
使用手机观看 | 其它方式观看 | 合计 | |
男学生 | 20 | 8 | 28 |
女学生 | 20 | 12 | 32 |
合计 | 40 | 20 | 60 |
(1)估计该校高三学生当天的观看人数.
(2)当天没有观看的5名学生中,有3人第二天观看了重播.从这5名学生中任选2人求这2人第二天都看了重播的概率;
(3)根据列联表判断,能否有95%的把握认为网络观看的学生中“是否使用手机观看”与“学生的性别”有关?
附: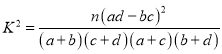 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 首项和公差都是
首项和公差都是![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,等比数列
,等比数列![]() 各项均为正数,公比为q,记
各项均为正数,公比为q,记![]() 的前n项和为
的前n项和为![]() :
:
(1)写出![]()
![]() 构成的集合A;
构成的集合A;
(2)若将![]() 中的整数项按从小到大的顺序构成数列
中的整数项按从小到大的顺序构成数列![]() ,求
,求![]() 的一个通项公式;
的一个通项公式;
(3)若q为正整数,问是否存在大于1的正整数k,使得![]()
![]() 同时为(1)中集合A的元素?若存在,写出所有符合条件的
同时为(1)中集合A的元素?若存在,写出所有符合条件的![]() 的通项公式,若不存在,请说明理由.
的通项公式,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com