
【题目】用另一种方法表示下列集合.
(1){x||x|≤2,x∈Z};
(2){能被3整除,且小于10的正数};
(3)坐标平面内在第四象限的点组成的集合.
(4){(x,y)|x+y=6,x,y均为正整数};
(5){-3,-1,1,3,5}.
(6)被3除余2的正整数集合.
【答案】(1){-2,-1,0,1,2} (2){3,6,9}
(3) ![]()
(4){(1,5),(2,4),(3,3),(4,2),(5,1)}
(5){x|x=2k-1,-1≤k≤3,k∈Z}
(6){x|x=3n+2,n∈N}
【解析】试题分析:(1)用列举法表示;(2)用列举法;(3)描述法写出;(4)用列举法列举出元素即可;(5)部分奇数构成的集合,用描述法写出;(6)描述法写出 .
试题解析:
(1){-2,-1,0,1,2} (2){3,6,9}
(3) ![]()
(4){(1,5),(2,4),(3,3),(4,2),(5,1)}
(5){x|x=2k-1,-1≤k≤3,k∈Z}
(6){x|x=3n+2,n∈N}


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】设f(x)为定义在R上的奇函数.如图是函数图象的一部分,当0≤x≤2时,是线段OA;当x>2时,图象是顶点为P(3,4)的抛物线的一部分.
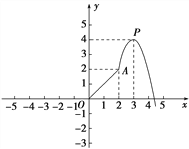
(1)在图中的直角坐标系中画出函数f(x)的图象;
(2)求函数f(x)在[2,+∞)上的解析式;
(3)写出函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度x的一次函数.
是车流密度x的一次函数.
①当![]() 时,求函数
时,求函数![]() 的表达式.
的表达式.
②当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com