
设函数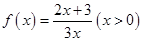 ,数列
,数列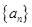 满足
满足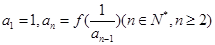 .
.
⑴求数列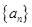 的通项公式;
的通项公式;
⑵设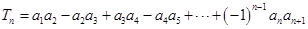 ,若
,若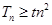 对
对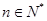 恒成立,求实数
恒成立,求实数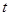 的取值范围;
的取值范围;
⑶是否存在以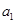 为首项,公比为
为首项,公比为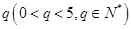 的数列
的数列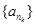 ,
,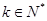 ,使得数列
,使得数列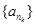 中每一项都是数列
中每一项都是数列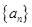 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列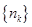 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
(1)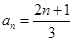 ;(2)
;(2)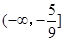 ;(3)存在,理由详见解析.
;(3)存在,理由详见解析.
解析试题分析:(1)将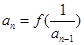 利用
利用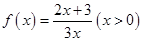 进行化简,得到关于
进行化简,得到关于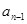 与
与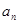 的递推关系式,根据其特点,求其通项公式;(2)本题关键是求出
的递推关系式,根据其特点,求其通项公式;(2)本题关键是求出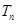 ,根据其表达式的特点,可每两项组合后提取公因式
,根据其表达式的特点,可每两项组合后提取公因式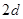 后,转化为等差数列求和,但要注意对
后,转化为等差数列求和,但要注意对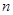 ,分奇偶性讨论,求出
,分奇偶性讨论,求出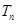 后,
后,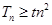 对
对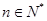 恒成立再分离参数后转化为求最值问题,容易求出实数
恒成立再分离参数后转化为求最值问题,容易求出实数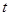 的取值范围;(3)此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.
的取值范围;(3)此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.
试题解析:⑴因为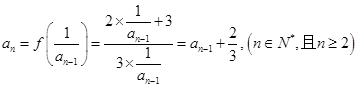 ,
,
所以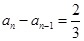 . 2分
. 2分
因为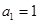 ,所以数列
,所以数列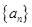 是以1为首项,公差为
是以1为首项,公差为 的等差数列.
的等差数列.
所以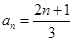 . 4分
. 4分
⑵①当 时,
时,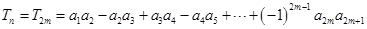
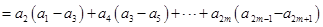
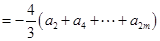
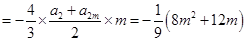
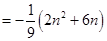 . 6分
. 6分
②当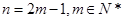 时,
时,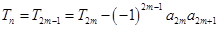
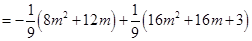
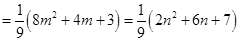 . 8分
. 8分
所以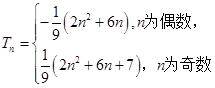 要使
要使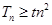 对
对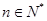 恒成立,
恒成立,
只要使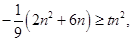
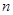 为偶数恒成立.
为偶数恒成立.
只要使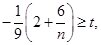 ,
,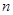 为偶数恒成立,故实数
为偶数恒成立,故实数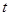 的取值范围为
的取值范围为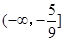 . 10分
. 10分
⑶由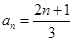 ,知数列
,知数列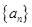 中每一项都不可能是偶数.
中每一项都不可能是偶数.
①如存在以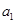 为首项,公比
为首项,公比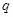 为2或4的数列
为2或4的数列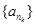 ,
,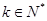 ,
,
此时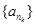 中每一项除第一项外都是偶数,故不存在以
中每一项除第一项外都是偶数,故不存在以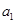 为首项,公比为偶数的数列
为首项,公比为偶数的数列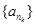 . 12分
. 12分
②当 时,显然不存在这样的数列
时,显然不存在这样的数列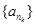 .
.
当 时,若存在以
时,若存在以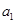 为首项,公比为3的数列
为首项,公比为3的数列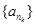 ,
,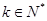 .
.
则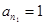 ,
,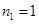 ,
,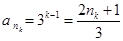 ,
,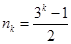 .
.
所以满足条件的数列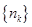 的通项公式为
的通项公式为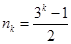 . 16分
. 16分
考点:等差数列、等比数列与函数、不等式的综合运用.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
已知an=n×0.8n(n∈N*).
(1)判断数列{an}的单调性;
(2)是否存在最小正整数k,使得数列{an}中的任意一项均小于k?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线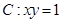 ,过
,过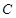 上一点
上一点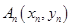 作一斜率为
作一斜率为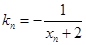 的直线交曲线
的直线交曲线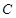 于另一点
于另一点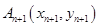 (
(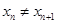 且
且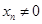 ,点列
,点列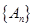 的横坐标构成数列
的横坐标构成数列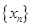 ,其中
,其中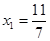 .
.
(1)求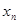 与
与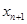 的关系式;
的关系式;
(2)令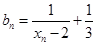 ,求证:数列
,求证:数列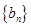 是等比数列;
是等比数列;
(3)若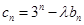 (
( 为非零整数,
为非零整数,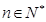 ),试确定
),试确定 的值,使得对任意
的值,使得对任意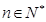 ,都有
,都有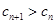 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知{an}是等差数列,a1=3,Sn是其前n项和,在各项均为正数的等比数列{bn}中,b1=1,且b2+S2=10,S5 =5b3+3a2.
(I )求数列{an}, {bn}的通项公式;
(II)设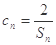 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证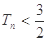
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 是等差数列,且
是等差数列,且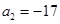 ,
,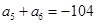 ;又若
;又若 是各项为正数的等比数列,且满足
是各项为正数的等比数列,且满足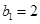 ,其前
,其前 项和为
项和为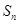 ,
,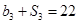 .
.
(1)分别求数列 ,
, 的通项公式
的通项公式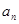 ,
,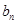 ;
;
(2)设数列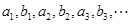 的前
的前 项和为
项和为 ,求
,求 的表达式,并求
的表达式,并求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列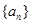 的各项均为正数,
的各项均为正数,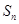 为其前
为其前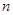 项和,对于任意的
项和,对于任意的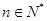 ,满足关系式
,满足关系式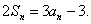
(1)求数列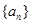 的通项公式;
的通项公式;
(2)设数列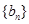 的通项公式是
的通项公式是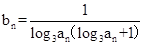 ,前
,前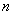 项和为
项和为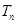 ,求证:对于任意的正整数
,求证:对于任意的正整数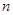 ,总有
,总有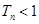 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com