
 =
= ,
, =
= ,
, =
= .试用向量法解下列问题:
.试用向量法解下列问题:
 |=|
|=|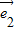 |=1,|
|=1,|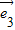 |=a,
|=a,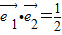 ,
,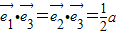 ,
,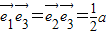 ,
,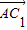 =
=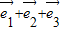 ,
,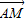 =
= (
(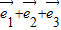 ),
),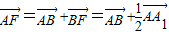 =
= +
+
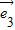 ,
,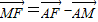 =
= (
(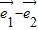 ),
),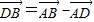 =
=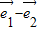 =2
=2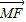 ,由此能证明直线MF∥平面ABCD.
,由此能证明直线MF∥平面ABCD.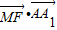 =(
=( )
)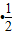
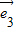 =0,
=0,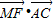 =(
=(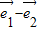 )(
)(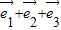 )
)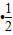 =0,知MF⊥AA1,MF⊥AC,AC和AA1是面ABCD内的相交直线,由此能证明直线MF⊥面A1ACC1.
=0,知MF⊥AA1,MF⊥AC,AC和AA1是面ABCD内的相交直线,由此能证明直线MF⊥面A1ACC1.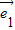 |=|
|=|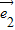 |=1,
|=1,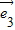 |=a,
|=a,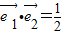 ,
,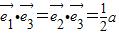 ,(2分)
,(2分)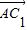 =
=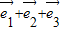 ,
,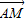 =
= (
( ),
),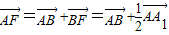 =
=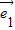 +
+
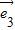 ,
,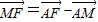 =
= (
(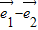 ),(3分)
),(3分)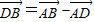 =
=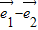 =2
=2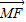 ,
, =(
=(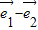 )
)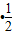
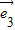 =0,(5分)
=0,(5分)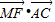 =(
=( )•(
)•(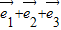 )
)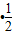 =0,(6分)
=0,(6分)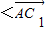 ,
,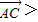
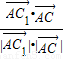
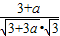 (12分)
(12分)

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
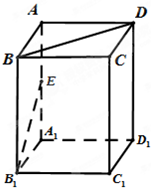 已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求
已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求查看答案和解析>>
科目:高中数学 来源: 题型:
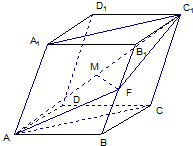 已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设
已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设| AB |
| e1 |
| AD |
| e2 |
| AA1 |
| e3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
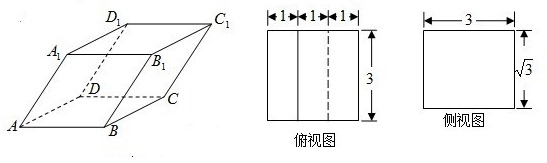 (2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为
(2012•江门一模)如图,已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形,侧视图是长为3宽为| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com