
(本小题12分)
四面体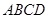 中,
中,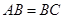 ,
,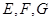 分别是
分别是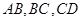 的中点,且
的中点,且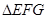 为正三角形,
为正三角形,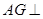 平面
平面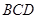 .
.
①求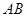 与平面
与平面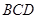 所成角的大小;
所成角的大小;
②求二面角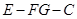 的平面角的余弦值.
的平面角的余弦值.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源:2014届安徽省高三第一次月考理科数学试卷(解析版) 题型:解答题
(本小题12分)如图:四棱锥P—ABCD中,底面ABCD

是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三上学期期末前月考文科数学试卷(解析版) 题型:解答题
(本小题12分) 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,
且∠A1AD=∠A1AB=60°。
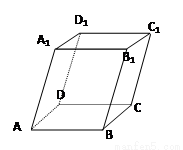
①求证四棱锥 A1-ABCD为正四棱锥;
②求侧棱AA1到截面B1BDD1的距离;
③求侧面A1ABB1与截面B1BDD1的锐二面角大小。
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二10月月考理科数学试卷(解析版) 题型:解答题
(本小题12分)如图,  、
、 分别是正四棱柱
分别是正四棱柱 上、下底面的中
上、下底面的中
心, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ当 取何值时,
取何值时, 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心?
的重心?

查看答案和解析>>
科目:高中数学 来源:2010年哈尔滨三中高一下学期第二模块数学卷 题型:解答题
(本小题12分)
四棱锥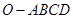 中,
中,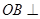 底面
底面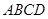 ,且
,且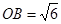 ,底面
,底面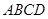 是菱形;点
是菱形;点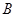 在平面
在平面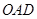 内的射影
内的射影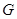 恰为
恰为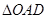 的重心.
的重心.
 ①求
①求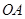 的长;
的长;
②求二面角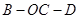 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年海南省高二下学期质量检测数学文卷(一) 题型:解答题
.(本小题12分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:

|
零件的个数 |
2 |
3 |
4 |
5 |
|
加工的时间 |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散点图;
(2)求 关于
关于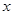 的线性回归方程
的线性回归方程 ;
;
(3)试预测加工10个零件需要多少时间?附: ,
, 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com