
【题目】已知f(x)=aln(x﹣1),g(x)=x2+bx,F(x)=f(x+1)﹣g(x),其中a,b∈R.
(1)若y=f(x)与y=g(x)的图象在交点(2,k)处的切线互相垂直,求a,b的值;
(2)若x=2是函数F(x)的一个极值点,x0和1是F(x)的两个零点,且x0∈(n,n+1)n∈N,求n.
【答案】
(1)解:f′(x)= ![]() ,g′(x)=2x+b,
,g′(x)=2x+b,
由题知 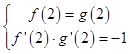 ,即
,即 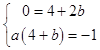 ,解得
,解得 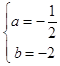
(2)解:F(x)=f(x+1)﹣g(x)=alnx﹣x2﹣bx,F ![]() .
.
由题知 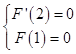 ,即
,即 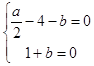 ,解得a=6,b=﹣1,
,解得a=6,b=﹣1,
∴F(x)=6lnx﹣x2+x,F ![]() =
= ![]() ,
,
∵x>0,由F′(x)>0,解得0<x<2;由F′(x)<0,解得x>2,
∴F(x)在(0,2)上单调递增,在(2,+∞)单调递减,
故F(x)至多有两个零点,其中x1∈(0,2),x2∈(2,+∞),
又F(2)>F(1)=0,F(3)=6(ln3﹣1)>0,F(4)=6(ln4﹣2)<0,
∴x0∈(3,4),故n=3
【解析】(1)根据导数的几何意义建立切线斜率之间的关系建立方程,求a,b的值;(2)根据导数和函数极值之间的关系建立方程,即可求n;
【考点精析】通过灵活运用函数的极值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】我国的高铁技术发展迅速,铁道部门计划在![]() 两城市之间开通高速列车,假设列车在试运行期间,每天在
两城市之间开通高速列车,假设列车在试运行期间,每天在![]() 两个时间段内各发一趟由
两个时间段内各发一趟由![]() 城开往
城开往![]() 城的列车(两车发车情况互不影响),
城的列车(两车发车情况互不影响),![]() 城发车时间及概率如下表所示:
城发车时间及概率如下表所示:
发车 时间 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
若甲、乙两位旅客打算从![]() 城到
城到![]() 城,他们到达
城,他们到达![]() 火车站的时间分别是周六的
火车站的时间分别是周六的![]() 和周日的
和周日的![]() (只考虑候车时间,不考虑其他因素).
(只考虑候车时间,不考虑其他因素).
(1)设乙候车所需时间为随机变量![]() (单位:分钟),求
(单位:分钟),求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求甲、乙两人候车时间相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个圆柱形圆木的底面半径为1 m,长为10 m,将此圆木沿轴所在的平面剖成两部分.现要把其中一部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设![]() ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
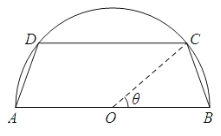
(1)求V关于θ的函数表达式;
(2)求![]() 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]()
D.若|z1|=|z2|,则z12=z22
查看答案和解析>>
科目:高中数学 来源: 题型:
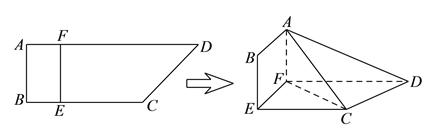
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com