
【题目】已知p:﹣x2+4x+12≥0,q:x2﹣2x+1﹣m2≤0(m>0).
(Ⅰ)若p是q充分不必要条件,求实数m的取值范围;
(Ⅱ)若“¬p”是“¬q”的充分条件,求实数m的取值范围.
【答案】解:由题知:p为真时,由﹣x2+4x+12≥0得﹣2≤x≤6,
q为真时,由x2﹣2x+1﹣m2≤0(m>0).得1﹣m≤x≤1+m,
令P=[﹣2,6],Q=[1﹣m,1+m],m>0
(Ⅰ)∵p是q的充分不必要条件,∴PQ,
∴ ![]() ,等号不能同时取,得
,等号不能同时取,得 ![]() ,解得m≥5,
,解得m≥5,
故p是q充分不必要条件时,m取值范围是[5,+∞)
(Ⅱ)∵“¬p”是“¬q”的充分条件,
∴“p”是“q”的必要条件,
∴QP,∴  ,解得0<m≤3,
,解得0<m≤3,
∴m的取值范围是(0,3]
【解析】(Ⅰ)求出p,q的等价条件,结合充分不必要条件的定义建立集合关系进行求解即可.(Ⅱ)根据逆否命题的等价性进行转化,结合充分条件和必要条件的定义进行转化解不等式组即可.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知学生的总成绩与数学成绩之间有线性相关关系,下表给出了5名同学在一次考试中的总成绩和数学成绩(单位:分).
学生编号 成绩 | 1 | 2 | 3 | 4 | 5 |
总成绩/x | 482 | 383 | 421 | 364 | 362 |
数学成绩/y | 78 | 65 | 71 | 64 | 61 |
(1)求数学成绩与总成绩的回归直线方程.
(2)根据以上信息,如果一个学生的总成绩为450分,试估计这个学生的数学成绩;
(3)如果另一位学生的数学成绩为92分,试估计其总成绩是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC⊥AB,AB=2AA1 , M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点. 
(1)若DE∥平面A1MC1 , 求 ![]() ;
;
(2)求直线BC和平面A1MC1所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
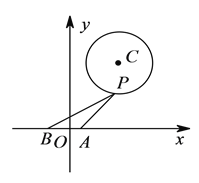
【题目】如图,在平面直角坐标系内,已知点A(1,0,B(-1,0),圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点.
为圆上的动点.
(1)求过点![]() 的圆
的圆![]() 的切线方程.
的切线方程.
(2)求![]() 的最大值及此时对应的点
的最大值及此时对应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2﹣x+2
(1)求函数f(x)的单调区间;
(2)求函数f(x)在[t,t+2](t>0)上的最小值;
(3)对一切的x,2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若1+ ![]() =
= ![]() .
.
(1)求角A的大小;
(2)若函数f(x)=2sin2(x+ ![]() )﹣
)﹣ ![]() cos2x,x∈[
cos2x,x∈[ ![]() ,
, ![]() ],在x=B处取到最大值a,求△ABC的面积.
],在x=B处取到最大值a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cosB= ![]() ,tanC=
,tanC= ![]() . (Ⅰ)求tanB和tanA;
. (Ⅰ)求tanB和tanA;
(Ⅱ)若c=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的减函数,其导函数f′(x)满足 ![]() +x<1,则下列结论正确的是( )
+x<1,则下列结论正确的是( )
A.对于任意x∈R,f(x)<0
B.对于任意x∈R,f(x)>0
C.当且仅当x∈(﹣∞,1),f(x)<0
D.当且仅当x∈(1,+∞),f(x)>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com