设函数
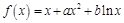
,曲线
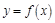
过点
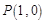
,且在
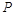
点处的切线斜率为2.
(1)求a和b的值; (2)证明:
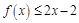
.
(1)
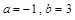
; (2)详见试题解析.
试题分析:(1) 首先由曲线
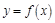
过点
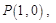
列方程求得
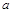
的值.再求
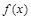
的导数,利用导数的几何意义得
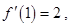
列方程,解这个方程即可得
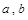
的值;(2) 由(1)可得
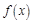
的解析式
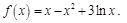
要证
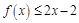
,构造函数
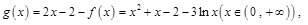
只要证
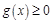
在
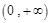
恒成立即可,为此可利用导数求函数
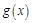
在
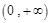
上的最小值,通过
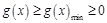
,来证明
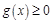
,进而证明
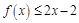
.
试题解析:(1)解:
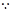
曲线
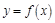
过点
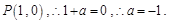
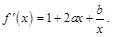
又曲线在
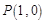
点处的切线斜率为2,
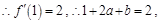
把
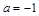
代入上式得
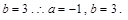
(2)证明:由(1)得
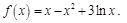
要证
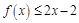
,构造函数
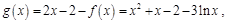
只要证
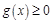
在
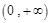
恒成立即可.
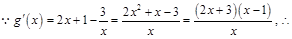
当
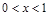
时,
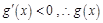
在
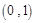
内是减函数;
当
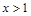
时,
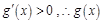
在
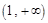
上是增函数,
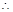
当
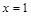
时,
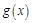
取最小值
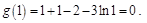
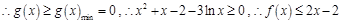
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
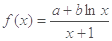
在点
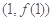
处的切线方程为
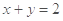
.
(1)求
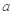
,
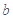
的值;
(2)对函数
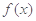
定义域内的任一个实数
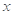
,
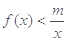
恒成立,求实数
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)已知函数
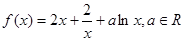
.
(1)若函数
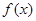
在
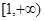
上单调递增,求实数
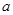
的取值范围.
(2)记函数
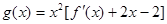
,若
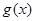
的最小值是

,求函数
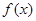
的解析式.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
直线
y=
kx+
b与曲线
y=
x3+
ax+1相切于点(2,3),则
b的值为( ).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
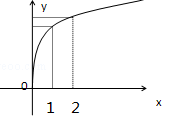
函数
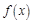
的图象如图,
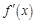
是
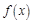
的导函数,则下列数值排列正确的是 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若曲线
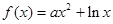
上存在垂直y轴的切线,则实数a的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
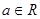
,函数
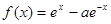
的导函数为
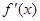
,且
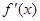
是奇函数,则
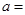
( )
| A.0 | B.1 | C.2 | D.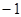 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知点P在曲线
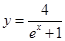
上,
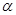
为曲线在点P处的切线的倾斜角,则
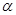
的取值范围是( )
查看答案和解析>>

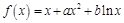 ,曲线
,曲线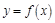 过点
过点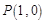 ,且在
,且在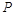 点处的切线斜率为2.
点处的切线斜率为2.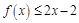 .
. 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案