
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明![]() )在
)在![]() )上的单调性;
)上的单调性;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 为奇函数;(2)证明见解析;(3)
为奇函数;(2)证明见解析;(3)![]() .
.
【解析】试题分析:
本题考查函数奇偶性的判断和单调性的证明,以及根据恒成立问题求参数取值范围。(1)根据奇偶性的判断方法证明。(2)根据单调性的判断方法证明。(3)根据函数的单调性将函数不等式转化为一般不等式,通过分离参数的方法转化为求具体函数的最值问题处理。
试题解析:
(1)![]() 定义域R关于原点对称,
定义域R关于原点对称,
∵ ,
,
![]() 为奇函数.
为奇函数.
(2)证明:设![]() R,且
R,且![]() ,
,
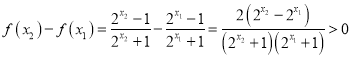 ,
,
∵函数 ![]() 在
在 ![]() 上为增函数,
上为增函数,
![]() ,故
,故![]() ,
,
![]() .
.
∴函数![]() 在
在![]() 上是增函数 .
上是增函数 .
(3)![]()
![]() ,
,
又![]() 为奇函数,
为奇函数,
![]() ,
,
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上为增函数,
上为增函数,
∴当![]() 时,函数
时,函数![]() 取得最小值,且
取得最小值,且![]() 。
。
∴![]() 。
。
故实数![]() 的取值范围为
的取值范围为![]() 。
。


科目:高中数学 来源: 题型:
【题目】甲、乙两人从1,2,…,15这15个数中,依次任取一个数(不放回).则在已知甲取到的数是5的倍数的情况下,甲所取的数大于乙所取的数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地西红柿从![]() 月
月![]() 日起开始上市.通过市场调查,得到西红柿种植成本
日起开始上市.通过市场调查,得到西红柿种植成本![]() (就是每
(就是每![]() 公斤西红柿的种植成本,单位:元)与上市时间
公斤西红柿的种植成本,单位:元)与上市时间![]() (单位:天)的数据如下表:
(单位:天)的数据如下表:
上市时间 | 50 | 110 | 250 |
种植成本 | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本与上市时间![]() 的变化关系:
的变化关系:![]() ;
;![]() ;
;![]() ;
;![]() ,并求出函数解析式;
,并求出函数解析式;
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=﹣x+1与椭圆 ![]() +
+ ![]() =1(a>b>0)相交于A、B两点.
=1(a>b>0)相交于A、B两点.
(1)若椭圆的离心率为 ![]() ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量 ![]() 与向量
与向量 ![]() 互相垂直(其中O为坐标原点),当椭圆的离心率e∈[
互相垂直(其中O为坐标原点),当椭圆的离心率e∈[ ![]() ,
, ![]() ]时,求椭圆的长轴长的最大值.
]时,求椭圆的长轴长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 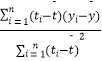 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:4x+y-4=0,l2:mx+y=0,l3:2x-3my-4=0.
(1)若直线l1,l2,l3交于一点,求实数m的值;
(2)若直线l1,l2,l3不能围成三角形,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com