练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法正确的是(　　)

    A. 若命题都是真命题,则命题“”为真命题

    B. 命题“”的否定是“,”

    C. 命题:“若,则或”的否命题为“若,则或”

    D. “”是“”的必要不充分条件

    【答案】B

    【解析】

    A．由复合命题的真假进行判断；

    B．利用全称命题的否定即可判断出；

    C． 利用命题的否命题形式即可判断出；

    D．由充分必要条件的定义进行判断．

    A．命题p，￢q都是真命题，则命题q为假命题，因此“p∧q”为假命题，因此不正确；

    B．“x∈R，2x＞0”的否定是“x0∈R，0”，正确；

    C． “若xy＝0，则x＝0或y＝0”的否命题为“若xy≠0则x≠0且y≠0”，因此不正确；

    D．“x＝﹣1”是“x2﹣5x﹣6＝0”的充分不必要条件，因此不正确，

    综上可得：只有B正确．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，所有学生的成绩均在区间内，其频率分布直方图如图．

    （Ⅰ）求获得复赛资格的人数；

    （Ⅱ）从初赛得分在区间的参赛者中，利用分层抽样的方法随机抽取人参加学校座谈交流，那么从得分在区间与各抽取多少人?

    （Ⅲ）从（Ⅱ）抽取的人中，选出人参加全市座谈交流，设表示得分在区间中参加全市座谈交流的人数，求的分布列及数学期望E（X）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元。

    （Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，）的函数解析式；

    （Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得下表：

    周需求量n

    18

    19

    20

    21

    22

    频数

    1

    2

    3

    3

    1

    以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台机床生产的零件各100件进行检测，检测结果统计如下：

    测试指标

    [85，90）

    [90，95）

    [95，100）

    [100，105）

    [105，110）

    甲机床

    8

    12

    40

    32

    8

    乙机床

    7

    18

    40

    29

    6

    （1）试分别估计甲机床、乙机床生产的零件为优品的概率；

    （2）甲机床生产1件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元，假设甲机床某天生产50件零件，请估计甲机床该天的利润（单位：元）；

    （3）从甲、乙机床生产的零件指标在[90，95）内的零件中，采用分层抽样的方法抽取5件，从这5件中任意抽取2件进行质量分析，求这2件都是乙机床生产的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种设备随着使用年限的增加，每年的维护费相应增加现对一批该设备进行调查，得到这批设备自购入使用之日起，前五年平均每台设备每年的维护费用大致如表：

    年份年

    1

    2

    3

    4

    5

    维护费万元

    Ⅰ求y关于t的线性回归方程；

    Ⅱ若该设备的价格是每台5万元，甲认为应该使用满五年换一次设备，而乙则认为应该使用满十年换一次设备，你认为甲和乙谁更有道理？并说明理由．

    参考公式：，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线 （a>0,b>0）的右焦点为，右顶点为A，过F作的垂线与双曲线交于、两点，过分别作的垂线，两垂线交于点，若到直线的距离小于， 则双曲线的渐近线斜率的取值范围是

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A（t，1）为函数y＝ax2+bx+4（a，b为常数，且a≠0）与y＝x图象的交点．

    （1）求t；

    （2）若函数y＝ax2+bx+4的图象与x轴只有一个交点，求a，b；

    （3）若1≤a≤2，设当≤x≤2时，函数y＝ax2+bx+4的最大值为m，最小值为n，求m﹣n的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业2017年的纯利润为500万元，因设备老化等原因，企业的生产能力逐年下降，若不能进行技术改造，预测从2018年起每年比上一年纯利润减少20万元，2018年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第年（以2018年为第一年）的利润为万元（为正整数）.

    （1）设从今年起的前年，若该企业不进行技术改造的累计纯利润为万元，进行技术改造后的累计纯利润为万元（须扣除技术改造资金），求，的表达式；

    （2）依上述预测，从2018年起该企业至少经过多少年，进行技术改造后的累计利润超过不进行技术改造的累计纯利润？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，已知直线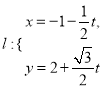（为参数），曲线（为参数），以原点为极点， 轴的正半轴为极轴建立坐标系.

    （1）写出直线的普通方程与曲线的极坐标方程；

    （2）设直线与曲线交于， 两点，求的面积.

    查看答案和解析>>

    同步练习册答案