
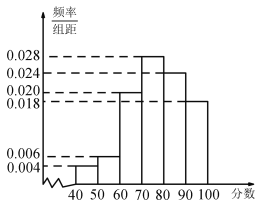
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
【答案】(1)![]() ;77.14;(2)
;77.14;(2)![]() .
.
【解析】
(1)由题意列出频率分布表,求和即可估计该地区用户对该电讯企业评分不低于70分的概率;利用中位数两侧的概率和相等列方程即可估计对该电讯企业评分的中位数;
(2)由题意计算出受调查用户评分在![]() 、
、![]() 的人数,求出总的基本事件个数及满足要求的基本事件的个数,由古典概型概率公式即可得解.
的人数,求出总的基本事件个数及满足要求的基本事件的个数,由古典概型概率公式即可得解.
(1)由题意,该地区用户对该电讯企业评分的频率分布如下表:
评分 |
|
|
|
|
|
|
频率 | 0.04 | 0.06 | 0.20 | 0.28 | 0.24 | 0.18 |
因此可估计评分不低于70分的概率为![]() ;
;
对该电讯企业评分的中位数设为x,可得![]() ,
,
则![]() ,
,
解得![]() ,
,
所以可估计对该电讯企业评分的中位数为![]() ;
;
(2)受调查用户评分在![]() 的有
的有![]() 人,
人,
若编号依次为1,2,3,4,从中选2人的事件有![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
共有![]() 个基本事件;
个基本事件;
受调查用户评分在![]() 的有
的有![]() 人,
人,
若编号依次为1,2,3,..9,10,从中选2人,
可得共有![]() 个基本事件;
个基本事件;
因此2人评分都在![]() 的概率
的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)在(﹣∞,0]上单调递增,且f(﹣1)=﹣1.若f(x﹣1)+1≥0,则x的取值范围是_____;设函数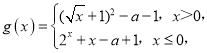 若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
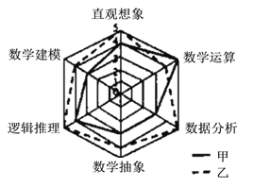
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上一动点A的坐标为![]() .
.
(1)求点A的轨迹E的方程;
(2)点B在轨迹E上,且纵坐标为![]() .
.
(i)证明直线AB过定点,并求出定点坐标;
(ii)分别以A,B为圆心作与直线![]() 相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得
相切的圆,两圆公共弦的中点为H,在平面内是否存在定点P,使得![]() 为定值?若存在,求出点P坐标;若不存在,请说明理由.
为定值?若存在,求出点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
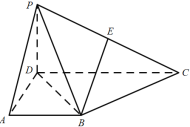
【题目】
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() =90°,
=90°,![]() ,
,![]() .
.
(I)求证:![]()
![]() 平面
平面![]() ;
;
(II)求证:![]() 平面
平面![]() ;
;
(III)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为45°.
为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】骰子,古代中国民间娱乐用来投掷的博具,早在战国时期就有.最常见的骰子是正六面体,也有正十四面体、球形十八面体等形制的骰子,如图是满城汉墓出土的铜茕,它是一个球形十八面体骰子,有十六面刻着一至十六数字,另两面刻“骄”和“酒来”,其中“骄”表示最大数十七,“酒来”表示最小数零,每投一次,出现任何一个数字都是等可能的.现投掷铜茕三次观察向上的点数,则这三个数能构成公比不为1的等比数列的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com