
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
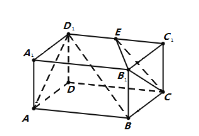
(1)在所给图中画出平面![]() 与平面
与平面![]() 的交线(不必说明理由)
的交线(不必说明理由)
(2)证明:![]() 平面
平面![]()
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系x-O-y中,已知曲线E:![]() (t为参数)
(t为参数)
(1)在极坐标系O-x中,若A、B、C为E上按逆时针排列的三个点,△ABC为正三角形,其中A点的极角θ=![]() ,求B、C两点的极坐标;
,求B、C两点的极坐标;
(2)在直角坐标系x-O-y中,已知动点P,Q都在曲线E上,对应参数分别为t=α与t=2α (0<α<2π),M为PQ的中点,求 |MO| 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
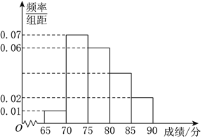
【题目】某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90).得到频率分布直方图如图C34.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用分层抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬传统文化,某市举办了“高中生诗词大赛”,现从全市参加比赛的学生中随机抽取![]() 人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为
人的成绩进行统计,得到如图所示的频率分布直方图,其中成绩的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() .
.
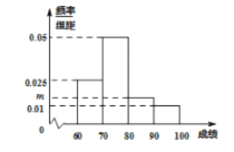
(1)求频率分布直方图中![]() 的值;
的值;
(2)在所抽取的![]() 名学生中,用分层抽样的方法在成绩为
名学生中,用分层抽样的方法在成绩为![]() 的学生中抽取了一个容量为
的学生中抽取了一个容量为![]() 的样本,再从该样本中任意抽取
的样本,再从该样本中任意抽取![]() 人,求
人,求![]() 人的成绩均在区间
人的成绩均在区间![]() 内的概率;
内的概率;
(3)若该市有![]() 名高中生参赛,根据此次统计结果,试估算成绩在区间
名高中生参赛,根据此次统计结果,试估算成绩在区间![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于其定义域
满足:对于其定义域![]() 内的任何一个自变量
内的任何一个自变量![]() ,都有函数值
,都有函数值![]() ,则称函数
,则称函数![]() 在
在![]() 上封闭.
上封闭.
(1)若下列函数:![]() ,
,![]() 的定义域为
的定义域为![]() ,试判断其中哪些在
,试判断其中哪些在![]() 上封闭,并说明理由.
上封闭,并说明理由.
(2)若函数![]() 的定义域为
的定义域为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 在其定义域
在其定义域![]() 上封闭?若存在,求出所有
上封闭?若存在,求出所有![]() 的值,并给出证明;若不存在,请说明理由.
的值,并给出证明;若不存在,请说明理由.
(3)已知函数![]() 在其定义域
在其定义域![]() 上封闭,且单调递增,若
上封闭,且单调递增,若![]() 且
且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com