
【题目】已知函数f(x)=2sinxcos(x-![]() ).
).
(Ⅰ)求函数f(x)的最小正周期.
(Ⅱ)当x∈[0, ![]() ]时,求函数f(x)的取值范围.
]时,求函数f(x)的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)f(x)∈[0,1+
;(Ⅱ)f(x)∈[0,1+![]() ].
].
【解析】试题分析:(Ⅰ)由两角差的余弦公式展开,结合二倍角公式化简得f(x)=sin(2x-![]() )+
)+![]() ,进而得周期;
,进而得周期;
(Ⅱ)由x∈[0, ![]() ]得2x-
]得2x-![]() ∈[-
∈[-![]() ,
,![]() ],即可得sin(2x-
],即可得sin(2x-![]() )∈[-
)∈[-![]() ,1],从而得解.
,1],从而得解.
试题解析:
因为f(x)=2sinx×cos(x-![]() ),
),
所以f(x)=2sinx×(cosxcos![]() +sinxsin
+sinxsin![]() )=sinx×cosx+
)=sinx×cosx+![]() sin2x=
sin2x=![]() sin2x+
sin2x+![]() (1-cos2x)=sin(2x-
(1-cos2x)=sin(2x-![]() )+
)+![]() .
.
(Ⅰ)函数f(x)的最小正周期为![]() .
.
(Ⅱ)因为x∈[0, ![]() ],所以2x-
],所以2x-![]() ∈[-
∈[-![]() ,
,![]() ].
].
所以sin(2x-![]() )∈[-
)∈[-![]() ,1].
,1].
所以f(x)∈[0,1+![]() ].
].


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数M,使得函数
,存在一个正数M,使得函数![]() 的值域包含于区间[-M,M]。例如,当
的值域包含于区间[-M,M]。例如,当![]() ,
, ![]() 时,
时, ![]() ,现有如下命题:
,现有如下命题:
①设函数![]() 的定义域为D,则“
的定义域为D,则“![]() ”的充要条件是“
”的充要条件是“![]() ”;
”;
②若函数![]() ,则
,则![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
, ![]() 的定义域相同,且
的定义域相同,且![]() ,
, ![]() ,则
,则![]()
④若函数![]() ,则
,则![]() 有最大值且
有最大值且![]() ,
,
其中的真命题有_____________。(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙,丙,丁四名同学做传递手帕游戏(每位同学传递到另一位同学记传递1次),手帕从甲手中开始传递,经过5次传递后手帕回到甲手中,则共有__________种不同的传递方法.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ;
;
②![]() .
.
(![]() )分别写出一个单调递增的
)分别写出一个单调递增的![]() 阶和
阶和![]() 阶“期待数列”.
阶“期待数列”.
(![]() )若某
)若某![]() 阶“期待数列”是等差数列,求该数列的通项公式.
阶“期待数列”是等差数列,求该数列的通项公式.
(![]() )记
)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少汽车尾气排放,提高空气质量,各地纷纷推出汽车尾号限行措施.为做好此项工作,某市交警支队对市区各交通枢纽进行调查统计,表中列出了某交通路口单位时间内通过的1000辆汽车的车牌尾号记录:
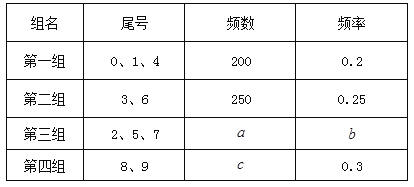
由于某些数据缺失,表中以英文字母作标识.请根据图表提供的信息计算:
(Ⅰ)若采用分层抽样的方法从这1000辆汽车中抽出20辆,了解驾驶员对尾号限行的建议,应分别从一、二、三、四组中各抽取多少辆?
(Ⅱ)以频率代替概率,在此路口随机抽取4辆汽车,奖励汽车用品.用![]() 表示车尾号在第二组的汽车数目,求
表示车尾号在第二组的汽车数目,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为( )
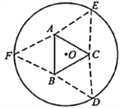
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,D,E,F分别为PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
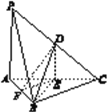
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com