
【题目】如图,在三棱锥D-ABC中![]() 为锐角三角形,平面ACD⊥平面
为锐角三角形,平面ACD⊥平面![]() .
.
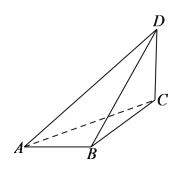
(1)求证:CD⊥平面ABC
(2)若直线BD与平面ACD所成角的正弦值为![]() ,求二面角D-AB-C的余弦值.
,求二面角D-AB-C的余弦值.
科目:高中数学 来源: 题型:
【题目】“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,下表是2013-2017年全国快递业务量(x亿件:精确到0.1)及其增长速度(y%)的数据
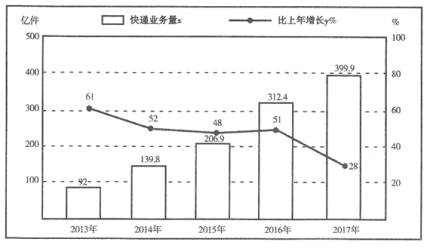
(1)试计算2012年的快递业务量;
(2)分别将2013年,2014年,…,2017年记成年的序号t:1,2,3,4,5;现已知y与t具有线性相关关系,试建立y关于t的回归直线方程![]() ;
;
(3)根据(2)问中所建立的回归直线方程,估算2019年的快递业务量
附:回归直线的斜率和截距地最小二乘法估计公式分别为: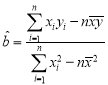 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
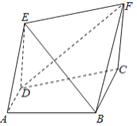
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一题:今有牛、马、羊食人苗,苗主责之粟四斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?其意是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿4斗粟,羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,牛、马、羊的主人各应赔偿多少粟?在这个问题中,牛主人比羊主人多赔偿了多少斗( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: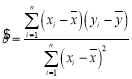 ,
,![]() ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com