
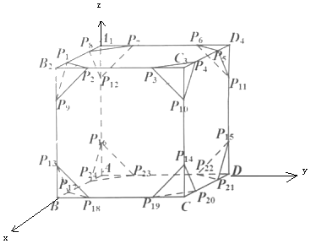
【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”,“灯者立方去其八角也”,如图所示,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点.
为棱上的四等分点.

(1)求该方灯体的体积;
(2)求直线![]() 和
和![]() 的所成角;
的所成角;
(3)求直线![]() 和平面
和平面![]() 的所成角.
的所成角.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)计算出八个角(即八个三棱锥)的体积之和,然后利用正方体的体积减去这八个角的体积之和即可得出方灯体的体积;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用空间向量法求出直线
轴,建立空间直角坐标系,利用空间向量法求出直线![]() 和
和![]() 的所成角;
的所成角;
(3)求出平面![]() 的法向量,利用空间向量法求出直线
的法向量,利用空间向量法求出直线![]() 和平面
和平面![]() 的所成角的正弦值,由此可得出
的所成角的正弦值,由此可得出![]() 和平面
和平面![]() 的所成角的大小.
的所成角的大小.
(1)![]() 在棱长为
在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点,
为棱上的四等分点,
![]() 该方灯体的体积:
该方灯体的体积:![]() ;
;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,
,
设直线![]() 和
和![]() 的所成角为
的所成角为![]() ,则
,则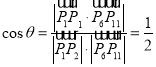 ,
,
![]() 直线
直线![]() 和
和![]() 的所成角为
的所成角为![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则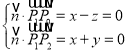 ,得
,得![]() ,取
,取![]() ,得
,得![]() ,
,
设直线![]() 和平面
和平面![]() 的所成角为
的所成角为![]() ,则
,则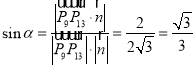 ,
,
![]() 直线
直线![]() 和平面
和平面![]() 的所成角为
的所成角为![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() 为直线
为直线![]() 的倾斜角.以坐标原点为极点,以
的倾斜角.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]()
B.当![]() ,
,![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]()
C.当![]() 时,不等式
时,不等式![]() 的解集可以为
的解集可以为![]() 的形式
的形式
D.不等式![]() 的解集恰好为
的解集恰好为![]() ,那么
,那么![]()
E.不等式![]() 的解集恰好为
的解集恰好为![]() ,那么
,那么![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)=![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①等式f(-x)=-f(x)在x∈R时恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三个根.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一、高二、高三的三个年级学生人数如下表
高三 | 高二 | 高一 | |
女生 | 100 | 150 | z |
男生 | 300 | 450 | 600 |
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(1)求z的值;
(2)用分层抽样的方法在高一中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1名女生的概率;
(3)用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下:9.4,8.6,9.2, 9.6,8.7,9.3,9.0,8.2,把这8人的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com