
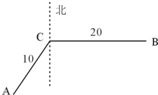
 如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.
如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.| AB |
| 3 |
| π |
| 4 |
| 3 |
| π |
| 6 |
| 3 |
| 7 |
| 7 |
| BC |
| sim? |
| AB |
| sim120° |
| 20 |
| sim? |
10
| ||
| sim120° |
| ||
| 7 |
| 3 |
| 7 |
| 3 |
1+cos(2x+
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| 3 |
| 3 |
| π |
| 12 |
| 5π |
| 12 |


科目:高中数学 来源: 题型:
 如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深BE=200 m,于C处测得水深CF=110 m,求∠DEF的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:
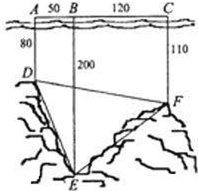 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,求∠DEF的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:
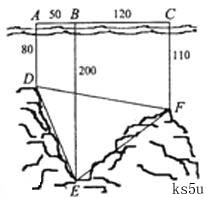 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知![]() ,
,![]() ,于A处测得水深
,于A处测得水深![]() ,于B处测得水深
,于B处测得水深![]() ,于C处测得水深
,于C处测得水深![]() ,求∠DEF的余弦值。
,求∠DEF的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
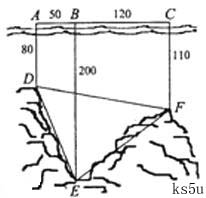 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知![]() ,
,![]() ,于A处测得水深
,于A处测得水深![]() ,于B处测得水深
,于B处测得水深![]() ,于C处测得水深
,于C处测得水深![]() ,求∠DEF的余弦值。
,求∠DEF的余弦值。 ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com